Suites numériques

 

 

Procédé de définition d’une suite

 

● X n  = f(n) .Si on connaît f la suite (X n ) est dite « explicitement définie » ou « explicite »

●Xn+1 = f(Xn) et on donne X0 . La suite (X n ) est définie par itération ou par récurrence.

●Xn+2 = f(Xn) + g(xn+1) et on donne X0 et X1. La suite (Xn) est définie par une récurrence à 2 termes.

 

Les suites explicites sont les plus faciles à étudier, il suffit souvent de les considérer comme une restriction de f(x) à N et l’étude de f(x) comme fonction sur R (sens de variation, limites en l’infini) nous donne des renseignements qui pourront être exploités dans l’étude de la suite.

Certaines suites récurrentes comme

la suite géométrique (Xn+1 = K Xn ) 

ou la suite arithmétique (Xn+1 =  Xn  + K)

peuvent être simplement ramenées à des suites explicites, mais ce n’est généralement pas le cas et il faudra alors recourir à des méthodes d’étude spécifiques.

 

Propriétés, vocabulaire et définitions

 

Sens de variation

Si sur un intervalle de N on a Xn < Xn+1 on dit que la suite est croissante. Si on a Xn+1 < Xn on dit que la suite est décroissante. On peut être amené à étudier le signe de Xn+1 – Xn ou à  comparer le module de  | Xn+1 / Xn| à 1 .

Une suite qui ne change pas de sens de variation sur un intervalle  de N est dite monotone sur cet intervalle.

 

Suites extraites

On peut être amené à considérer des suites extraites de (Xn) par restriction de l’indice à une partie infinie de N par exemple n impair

(n = 2p +1) ou n pair (n = 2p) .

 

Suites convergentes, divergentes

On dit qu’une suite est convergente si quand n → ∞,  lim (Xn) existe et prend une valeur finie .

Si ce n’est pas le cas, on dit qu’elle est divergente

 

● Si (Xn) a pour limite L, c’est aussi le cas de toute suite extraite de (Xn)

● Dans R, toute suite croissante et majorée (ou décroissante et minorée) est convergente

● Si Xn = f(n) ,  lim (Xn) si elle existe est égale à

● Si f(x) est continue en a , quand an est une suite qui converge vers a alors f(an) est une suite qui converge vers f(a) . La réciproque est vraie .

● Une suite de Cauchy est une suite telle que quel que soit ε , il existe un rang q tel que pour tous les rangs n et p supérieurs à q  on ait

d(Xn , Xp) < ε .

Une suite convergente est une suite de Cauchy. La réciproque est vraie dans R et C .

● Si deux suites  (Yn) et (Zn) ont des sens de variation inverses et que la suite (Yn–Zn) converge vers 0 , alors, on dit qu’elles sont adjacentes. Deux suites adjacentes convergent vers une même limite L.

● Si (Xn) et (Yn) sont 2 suites convergentes : Les suites suivantes sont convergentes : (Xn + Yn) , (λXn) , (XnYn) , (Xn/Yn) si lim (Yn) ≠ 0 , f(Xn) si f est continue en lim Xn. 

 

Comparaisons de suites  (à l’infini, à partir d’un rang donné)

(Xn) domine (Yn)                                 si Il existe λ non nul  tel que |Yn| ≤ λ|Xn|

(Xn) négligeable devant   (Yn)            si   lim(Xn / Yn) = 0        (Xn << Yn ou  Xn = o(Yn) )

(Xn) équivalente  à (Yn)                      si  lim (Xn – Yn) = 0  si           (Xn » Yn)

 

Exemple : à l’infini, on a   An <<  n! (on peut ne pas préciser à l’infini, c’est implicite )

 

Suites arithmétiques :

 

Récurrence : Xn+1 = Xn+ A et X0 est connu

 

D’où on tire Xn = X0 + nA  (suite explicite forcément divergente)

 

Somme de rang n : Sn = X0+ ….. + Xn =

 

Où (n+1) est le nombre de termes et (2 X0 + nA)  la somme du 1er et du dernier terme.

● remarque : somme des n premiers entiers : 1+2+….+n = n(n+1) / 2

 

Suites géométriques

 

Récurrence Xn+1 = RXn (R est appelé raison)  et X0 est connu

 

D’où on tire Xn = X0Rn  (suite explicite qui converge vers 0 si |R| < 1)

 

Somme de rang n Sn = X0+ ….. + Xn =          (n +1 est le nombre de termes)

 

● Si |R| < 1 , Sn converge vers

 

● remarque :   permet de factoriser xn+1–1

 

à rapprocher du DL de (au voisinage de 0 :  xn+1 tend vers 0)

 

 

Suites arithmético – géométriques

 

Récurrence  : Xn+1 = RXn + A et X0 est connu

C’est une suite géométrique si A = 0 et une suite arithmétique si R = 1

● Comment choisir K tel que Xn +K soit une suite géométrique de raison R? On trouve K =

 

● Le 1er terme de cette suite géométrique est X0 + K et on en tire Xn+K = (X0 + K)Rn d’où

Xn= (X0 + K)Rn – K   (Suite explicite)  avec K = A / (R – 1)

 

Récurrence linéaire à 2 termes

 

Récurrence linéaire à 2 termes : Xn+2 = AXn+1 + BXn   avec X0 et X1 donnés .

Si 2 suites vérifient cette relation avec les mêmes deux premiers termes, elles sont égales.

Il suffit d’en trouver une pour trouver la forme explicite.

Si on prend la suite Xn=krn+KRn

On a Xn+1=krn+1+KRn+1 et Xn+2=krn+2+KRn+2. Notre relation devient :

krn+2+KRn+2  = A(krn+1+KRn+1) + B(krn+KRn) =krn(Ar+B) + KRn (AR+B)

On identifie donc r2 =  Ar + B  et R2 = AR+B .

Donc r et R doivent être racines de l’équation

X2 – AX –B = 0  (on traite le cas de 2 racines réelle, las autres cas seront évoqués plus loin )

Quant à k et K on les identifie grâce aux « conditions initiales » :

X0 = k + K et X1 = kr + KR , système d’équations à 2 inconnues k et K (r et R étant connus)

 

● Finalement on a une forme explicite Xn=krn+KRn 

(ou krncos nθ +Krn sin nθ   si racines complexes ou krn +Knrn  si racine double )

Avec r et R racines de X2 – AX –B = 0 et k et K solutions de X0 = k + K et X1 = kr + KR

 

Exemple : suite de Fibonnacci :Xn+2 = Xn+1 + Xn,     X0 = 0   et X1 = 1

Equation X2 – X –1 = 0  solutions r =   et  R =

 

Equations 0 = k + K    et     1 = k + K         solutions k =  et K = –

En conclusion :  Xn = [  ()n – ()n ]  

 

Autres récurrences linéaires à 2 termes

 

Récurrence linéaire à 2 termes de type : Xn+2 = AXn+1 + BXn+C   avec X0 et X1 donnés .

Appelons SL (A, B, C) l’ensemble des suites qui vérifient l’équation sans vérifier les conditions initiales

 

● Appelons SL(A, B) l’ensemble des suites vérifiant Xn+2 = AXn+1 + BXn sans conditions initiales, on a vu qu’il suffisait de résoudre l’équation X2 – AX –B = 0 pour déterminer une base de  SL(A, B) { f(n) et F(n)}  telle que toute suite de SL(A, B) soit exprimée sous la forme   Xn = kf(n) + KF(n)

 

● On démontre facilement que si (Sn) est une suite de SL(A,B,C), on les obtient toutes en ajoutant à (Sn) une suite de SL(A, B).

Donc si (Xn) ∈ SL(A,B,C) : Xn = Sn + Yn avec Yn ∈∈SL(A,B)

 

● Prenons la suite constante Sn =λ. Elle appartient à SL(A,B,C) si λ = Aλ+Bλ+C soit

λ(1 – A – B)= C.

● Si A+B ≠ 1 , Sn = λ est la suite cherchée avec λ = C / (1 – A – B)

Nos solutions sont donc du type Xn = Yn + λ  et on sait trouver Yn par le procédé étudié dans l’exemple précédent.

Yn = kf(n) + KF(n) , Xn = kf(n) + KF(n)+   et les conditions initiales nous permettent de trouver k et K .

 

● Si A+B =1 On cherche un suite de type  Sn =λn qui appartienne à  SL(A,B,C) et on trouve

λ(2-A)=C. Soit λ = C / (2–A) pourvu que A soit différent de 2 quand B = – 1

 

● Si A+B =1 et A est différent de 2

On a A =B –1 , le polynôme caractéristique devient X2 – (B-1)X –B = 0 =(X-1)(X+B) et B ≠ –1

f(n) = 1n et F(n) = (–B)n  Donc les solutions sont de la forme λn + k +K(–B)n

Ce qui donne Xn =

 

● Si A+B = 1 et A = 2 c’est que B= –1 et on est obligé de chercher une suite Sn de la forme Sn =λn2.

Elle doit vérifier λ(n+2)2 = 2λ(n+1)2 – λn2 + C soit  2λ = C

L’équation caractéristique donne X2 -2X +1 = 0 ( une racine double X = 1)

Donc f(n) = 1n et f(n) = n1n. Ce qui donne Yn = k +Kn

Et Xn = Yn + λn2     Xn  =   k + Kn + n2

 

SYNTHESE

 

● Si une récurrence est de la forme générale  X n–2 – AXn–1 – BXn =  C

On retrouve la suite géométrique avec B = 0 et C = 0

La suite arithmético géométrique avec B = 0

La récurrence linéaire dans le cas général avec selon le cas C nul ou non nul

 

● Son polynôme caractéristique est X2 – AX – B = 0

 

On s’intéresse à ses racines non nulles et on trouve selon le cas

 

Nombre de solutions non nulles

Base des solutions

Type des solutions

f(n)

F(n)

Avec λ = 0 si C =0 et λ ¹ 0 si C ¹ 0

1 racine simple R

Rn

 

Xn = Kf(n) +λ

2 racines  r et R

rn

Rn

Si A+B ¹ 1             Xn = kf(n) + KF(n) + λ

Si A+B = 1 et A¹2  Xn = kf(n) + KF(n) + λn

Si A+B = 1 et A=2  Xn = kf(n) + KF(n) + λn2

2 racines Reiθ et Re–iθ

Rncos nθ

Rnsin nθ

1 racine double R

Rn

nRn

Xn  = λ (ou λn ou λn2) étant (par ordre de préférence) une suite qui vérifie la formule de récurrence

K et k étant déterminés par les conditions initiales (X0 et X1)

 

Il suffit de commencer par déterminer la suite stationnaire Sn = λ qui vérifie la formule, si elle n’existe pas on essaie la suite λn (puis λn2) ce qui fixe éventuellement des contraintes aux coefficients du  polynôme caractéristique. Puis ayant déterminé S n, f(n) et F(n) on peut écrire Xn=kf(n)+KF(n) + Sn. 

 

Suites définies par itération

 

Xn + 1 = f(Xn) avec f trop complexe pour trouver une formule explicite .

On dit que la suite est définie par itération de f

 

Interprétation graphique :

 

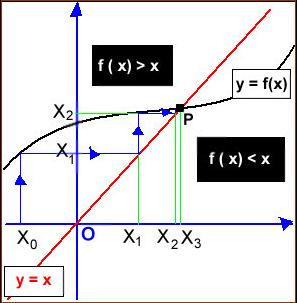On trace le graphe de f(x) et la droite d’équation y = x .

On prend X0 sur l’axe des X et on a X1 = f(X0)

Ensuite, on va chercher le point (X1 , X1) sur la droite et à sa verticale sur la courbe on a le point (X1 , X2 )

On réitère le procédé pour trouver le point (X2 , X2) sur la droite et à sa verticale on a le point (X2 , X3 )

Ainsi , de proche en proche ,on trouve sur la courbe les points d’ordonnée X1 , X2 , …. Xn et selon les configurations relatives de la courbe ou de la droite, ces points peuvent diverger ou converger vers un point précis de la courbe.

 

 

 

 

 

 

 

 

Notre but est d’étudier la divergence ou la convergence de la suite selon les paramètres de la configuration.

 

Critères de convergence :

● Il est clair que s’il existe un intervalle I de R tel que f(I) ⊂ I, et qu’il existe une valeur de n telle que Xn∈I alors f(Xn) ∈I et la série, pour tout rang supérieur à n,  est « prisonnière » dans cet intervalle qu’on appelle « Intervalle de stabilité »

 

● Par ailleurs si la fonction est continue et que Xn converge en L, on a on a lim Xn+1 = lim f(Xn) = f(lim Xn) et donc L = f(L) , ce qui signifie que si (Xn ) converge, c’est forcément à un point où f(x) = x , c'est-à-dire en un point d’intersection de la courbe et de la droite y = x .

Si un tel point existe, on dit que c’est un point fixe de f mais son existence ne garantit pas la convergence de (Xn ) . C’est une condition nécessaire mais pas suffisante.

● on va voir que la convergence dépend en fait de la valeur de la dérivée de f(x) au point où elle coupe la droite y = x :

Sur les dessins suivants, on a représenté la droite y = x en rouge  et le graphe de f(x) dans un voisinage du point fixe, qui peut donc être assimilé à la tangente en ce point (en noir) .

 

 

  Supposons la fonction croissante au point fixe :

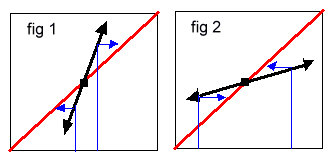
Figure 1 : quand la dérivée est > 1 , si Xn « tape » dans le voisinage du point fixe , la prochaine valeur Xn+1 qu’on va chercher sur la droite

y = x sera plus éloignée du point fixe que Xn.

Figure 2 : au contraire quand la dérivée est < 1 Xn+1 se rapproche du point fixe par rapport à Xn

 

  Supposons la fonction décroissante au point fixe:

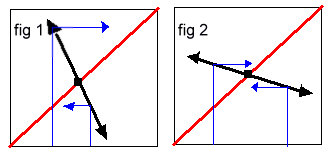
Figure 1 : quand la dérivée est < –1 , si Xn « tape » dans le voisinage du point fixe , la prochaine valeur Xn+1 qu’on va chercher sur la droite

y = x sera plus éloignée du point fixe que Xn.

Figure 2 : au contraire quand la dérivée est > – 1 alors Xn+1 se rapproche du point fixe par rapport à Xn

 

 

Donc, les conditions idéales de convergence sont réunies quand au point fixe L  –1 < f’(L) < 1

De plus, il est facile de comprendre que c’est seulement quand cette condition est vérifiée pour f’ qu’on a , pour un voisinage V de L 

f(V) ⊂ V  (stabilité) .

Il nous reste à résoudre plusieurs problème : Quelles sont les limites d’un intervalle de stabilité ? La situation d’un Xn dans un intervalle de stabilité autour du point fixe entraîne t – elle la convergence ? Dans quels cas, la situation d’un Xn dans un tel intervalle est – elle inéluctable ?

 

Suites récurrentes et fonctions croissantes ou décroissantes

● supposons f continue

     Si pour tout x ∈ [a ; b] f(x) > x alors f(b) > b  et f(b) ∉ [a ; b] (passage au limites si intervalle ouvert)

     Si pour tout x ∈ [a ; b] f(x) < x alors f(a) < a  et f(a) ∉ [a ; b] (passage au limites si intervalle ouvert)

Donc , si f, continue,  comporte un intervalle de stabilité , le graphe de f coupe la droite

y = x sur cet intervalle et il existe un point fixe L dans cet intervalle (tel que f(L) = L)

 

● Une fonction croissante vérifiant f(0) ≥ 0 et coupant la droite f(x) = x en x = L (L>0) possède un intervalle de stabilité [ 0 ,L] puisque

f([0,L]) ⊂ [ 0 , L] .

C’est le cas de  et x2 stables sur [0,1] 

x2 n’est pas stable sur  [a,1] avec 0< a < 1  puisque a2 < a

n’est pas stable sur [ 0,b]  avec 0  < b < 1 puisque > b

Dans les 2 cas, le retrait d’un point fixe de l’intervalle [0,1] dégrade son caractère « stable » .

 

● Soit un intervalle de stabilité [ a ; b ] pour f une fonction croissante sur [ a ; b ]

Si il existe c Î [ a ; b ] tel que f(c) > c alors l’intervalle de stabilité contient un point fixe L > c

En effet, si pour tout x ∈ [ c ; b ] on a f(x) > x  il vient que f(b) > b et b ne fait pas partie de l’intervalle de stabilité. On a donc forcément k>c tel que  f(k) ≤ k et la courbe coupe la droite y = x sur l’intervalle  [ c ; k ]. De même on démontre que :

Si il existe c Î [ a ; b ] tel que f(c) <c alors l’intervalle de stabilité contient un point fixe L < c

 

● Soit f une application croissante sur un intervalle de stabilité [a ; b], une suite  (Xn) définie par

Xn+1 = f(Xn) et comportant un terme dans cet intervalle, alors,  (Xn) est  monotone.

Si f(X0) –X0 > 0 , (1er point au dessus de la droite y = x) la suite est croissante.

Comme f(x) > x ⇒ x < L et que pour  x > L on a f(x) < x , la suite Xn est majorée par L  et comme une suite croissante et majorée converge, on a vu que c’était forcément  vers L

Si f(X0) –X0 < 0 , (1er point sous la droite y = x) la suite est décroissante.

f(x) < x ⇒ x > L et cette fois la suite est minorée par L donc elle converge vers L

Donc si f est croissante dans un intervalle de stabilité la suite récurrente converge vers L

Exemples : xn+1 =  stable sur [0 , b] avec b ≥ 1 croissante ou décroissante vers 1 selon qu’on prend  x0 < 1 ou  x0 > 1

xn+1 = (xn)2  stable sur [ 0 ; 1 ] n’est convergente et décroissante vers 0  que si l’on prend 0 ≤ x ≤ 1

 

● Si f est décroissante sur un intervalle de stabilité, les choses sont moins claires.

Mais il existes 2 suites extraites de Xn : X 2K et X 2K+1 (associées à f ○ f croissante) telles que chacune d’elles soit convergente. Xn ne converge que si elles ont la même limite (suites adhérentes).

 

Suites récurrentes et fonctions contractantes

 

● Soit f une fonction telle que |f(a) – f(b)| < k| a – b| avec K < 1 , sur un intervalle contenant a et b.

On dit qu’elle est contractante.

Remarquons que de f contractante on déduit  et donc –1 < f’(x) < 1

 

Remarquons que si f est telle que –1 < f’(x) < 1, le théorème des accroissements finis donne

 

 et donc  |f(a) – f(b)| < k| a – b| avec K = sup f’(x) sur l’intervalle. Donc :

 

 f contractante Û |f’(x)| < 1  

 

● Soit L un point fixe de f contractante et Xn définie par Xn+1 = f(Xn) .

Alors on a |f(L) – f(Xn)| < k| L– Xn| d’où on déduit  |L – Xn+1| < k| L– Xn|

Donc la suite | L– Xn| est décroissante et minorée par 0 , ce qui signifie qu’elle est convergente, de même que la suite Xn, et comme si Xn a une limite, il s’agit forcément de L . On en déduit que :

f contractante avec un point fixe en L  Þ Xn converge vers L

f est – elle contractante ? f admet –elle un point fixe ?  C’est le 1er test à réaliser quand on spécule sur la convergence d’une série définie par itération grâce à une fonction décroissante.