SERIES

● Par S_n = å U _i on entend somme des U _i pour 0≤ i ≤ n.

● Par R(S_n) ou R(å U _n) on entend å U _i pour n+1 ≤ i < ∞ (reste d’ordre n )

● Sn est dite alternée si le signe de U_i change selon une loi de type (-1)ⁱ

Certaines séries ne sont définies qu’à partir d’un certain rang :

série de Riemann dont série harmonique pour n ≥ 1

série de Bertrand pour n ≥ 2

● Par lim S_n = S , sauf précision il faut entendre lim s_n quand n → +∞ = S

● Une série est convergente (divergente) quand S_n, considérée comme une suite, est convergente (divergente) . Dans ce cas, il existe un nombre S fini tel que lim S_n = S

● On défini la série somme à partir de deux séries (S + T)_n = S_n + T_n

● on définit la série (λS)_n = λS_n

● Doté de ces deux lois (l’une interne, l’autre externe) l’ensemble des séries est un espace vectoriel dont le sous ensemble des séries convergentes est un sous espace vectoriel. Dans ce sous espace, l’application :

S_n → lim S_n est une application linéaire.

lim (S_n + T_n) = lim S_n + lim T_n et lim λS_n = λ lim S_n.

Série arithmétique S_n = U₀ + U₁ + .....+ U_n-1 + U_n (n+1 termes)

(produit du nombre de termes par la moyenne du premier et du dernier)

Série géométrique S_n = U₀ + U₀Q + U₀Q² + ……+ U₀Qⁿ (n + 1 termes)

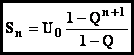on en déduit que pour x¹1 1+x+x²+...+xⁿ = (factorisation de 1-xⁿ)

convergence :

● Sn est convergente si sa limite existe

● Sn est absolument convergente si Σ |U_i| est convergente

● Un convergente ⇒ Lim U_i = 0

● Un convergente ⇒ Tout ε > 0 , ∃ r tel que tout n> r et tout p | 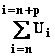| < ε ( Cauchy)

● Sn absolument convergente ⇒ Sn convergente

● Sn alternée et U_i → 0 ⇒ Sn convergente

Σ (1/n) série harmonique ne converge pas

Σ (–1)ⁿ(1/n) série harmonique alternée converge vers ln 2

Comparaison de séries de réels positifs

● en écrivant Un = f(n). f continue par morceaux converge ⇒ Sn convergente

● Si on peut écrire Un = f(n+1) – f(n) alors Sn = f(n) – f(0). f(n) converge ⇒ S(n) converge

Sans aller jusqu’à l’égalité, il suffit souvent d’encadrer Un grâce aux accroissements finis sur une primitive de f pour majorer et minorer Sn :

f(n) – f(n-1) ≤ Un ≤ f(n+1) – f(n)

Σ 1 / n^⍺ série de Riemann converge si et seulement si ⍺ > 1

Σ 1 / n(ln n)^⍺ série de Bertrand converge si et seulement si ⍺ > 1

● Si pour tout n 0 ≤ Un ≤ Vn : ΣVn converge ⇒ ΣUn converge et

ΣUn diverge ⇒ ΣVn diverge

● Si quand n → ∞ , ∃ ⍺ > 1 tel que lim n^⍺Un = 0 et n^⍺Un bornée , ΣUn converge

, ∃ ⍺ < 1 tel que 1/n^⍺ < Un , ΣUn diverge

● Si deux séries Un et Vn sont de signe constant à partir d’un certain rang et qu’à l’infini on ait Un ≈ Vn , (Un équivalent à Vn) les 2 séries sont de même nature.

On peut utiliser les développements limités à l’infini.

Exemple : 1/ n ² ≈ 1/ n – 1 / (n–1) . le reste de rang n tend vers 1 / n

●Si deux séries Un et Vn sont de signe positif à partir d’un certain rang et qu’à l’infini on ait

alors Un diverge ⇒ ΣVn diverge et ΣVn converge ⇒ ΣUn converge

Dans ce dernier cas, R(ΣUn) ≤ R(ΣVn)

● règle de d’Alembert .

◙ Si à partir d’un certain rang, il existe K tel que 0 < K < 1 et < K

alors ΣUn converge et R(ΣUn) ≤Un.

◙ Si K >1 et > K alors ΣUn diverge

◙ la règle reste valable si on prend K = lim (pour K = 1 , on ne peut rien dire)

● Séries et développements limités sont souvent imbriqués .