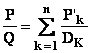POLYNOMES ET FONCTIONS RATIONNELLES

Le polynôme P=a_nXⁿ + …..+a₁X + a₀ peut être considéré comme un vecteur de coordonnées

(a_n, …..,a₀) dans la base {Xⁿ, …,X, 1} elle-même formée de polynômes qu’on appelle monômes.

Muni de l’addition et de la multiplication par un scalaire, l’ensemble de polynômes de degré ≤ n constitue un espace vectoriel

Qui est lui-même un sous espace vectoriel de l’ensemble des polynômes de degré ≤ n+1.

Par récurrence, on peut considérer l’ensemble des polynômes comme un espace vectoriel de dimension infinie qu’on appelle

R[X] ensemble des polynômes à coefficients réels.

Doté de l’addition et de la multiplication des polynômes R[X] a une structure d’anneau commutatif unitaire :

(R[X] , +) est un groupe commutatif. Distributivité du produit par rapport à +.

Produit commutatif et 1 = polynôme unité.

Le polynôme nul est celui dont les coefficients sont nuls.

● Les seuls polynômes inversibles sont de la forme a₀ = λ réel non nul .

●On appelle valuation de P le plus petit n pour lequel a_n est non nul (x³+5x² a pour valuation 2)

● On appelle monôme dominant de P son monôme de plus haut degré a_nXⁿ

● Si a_n = 1 on dit que le polynôme est unitaire.

Divisibilité

Un polynôme B divise un polynôme A si il existe un polynôme Q tel que A = BQ

Exemple : On peut écrire Xⁿ – aⁿ = (X–a) (X^n–1 + aX^n–2 + …+a^n–2X + a^n–1)

X²ⁿ⁺¹ + a²ⁿ⁺¹ = (X+a) (X²ⁿ – aX^2n–1 + a²X^2n–2–…–a^2n–1X + a²ⁿ)

Mais X²ⁿ+a²ⁿ n’est pas divisible par X+a

Dans R[X] , on a ⍺A divise A et A divise ⍺A donc le relation de divisibilité n’est pas antisymétrique.

Dans l’ensemble des polynômes unitaires ⍺A n’existe pas et la divisibilité est une relation d’ordre.

Division euclidienne de A par B

Il existe 2 polynômes Q et R uniques tels que A = BQ + R et degré de R < degré de Q

Si le degré de B est plus grand que le degré de B , alors Q = 0 et R = A .

Il faut, bien sûr que B ne soit pas nul .

Cette division s’effectue comme celle des décimaux :

En X⁴ combien de fois X² ? → X²

J’écris X² fois (X² +X + 1 à gauche).

Je soustrais (X⁴ +X³ +X² ) à (X⁴ · · )

J’écris le résultat à la ligne suivante (-X³ –X²)

Je descends · .

En –X³ combien de fois X² ? → – X et je recommence le processus. Je descends 1.

X+1 est de degré inférieur à 2 : c’est notre reste

X⁴ · · · + 1 X² +X + 1

X⁴ +X³ +X² X² – X

–X³ –X² ·

–X³ –X² –X

X +1

Je peux écrire X⁴ + 1 = (X² + X + 1) (X² – X) + (X+1)

Idéaux J de l’anneau R[X]

(J , +) est un sous groupe de (R[X], +) et, tout P ∈ J et tout p ∈R{X] : Pp ∈ J et pP ∈ J

Donc l’ensemble J des multiples de A donné est un idéal.

Pour A et B donnés, l’ensemble J des polynômes de la forme pA + p’B est un idéal

Il existe un polynôme unitaire D et un seul tels que J = { ensemble des multiples de D}

On dit que D engendre J .

Le degré de D est le plus petit degré des polynômes de J (ce degré existe forcément si J n’est pas vide) . Pour trouver D , il suffit de prendre un polynôme A de degré minimal de J et de le diviser par a_n son coefficient dominant. Si A ∈ J c’est aussi forcément le cas de D d’après la définition d’un idéal.

Soit A ∈J , sa division euclidienne par D donne A = DQ + R comme A et DQ ∈J c’est aussi le cas de A – DQ = R et comme R ne peut pas être de degré inférieur à celui de D on a R = 0.

Tous les polynômes de J sont donc divisibles par D et l’unicité de D coule de source.

● Soit J = { pA + p’B, quels que soient p∈R[x] et p’∈R[x] }

Alors, A ∈J et B∈J . Si D unitaire engendre J alors A et B sont des multiples de D .

Si il existe un polynôme unitaire D’ de degré supérieur à celui de D tel que A et B soient des multiples de D’ alors D’ engendre J ce qui est contradictoire avec l’unicité de D .

D est donc le PGCD de A et de B (ou plutôt le diviseur de plus haut degré commun à A et B)

Comme D ∈J, D peut être écrit sous la forme pA +p’B et en particulier,

si A et B sont premiers entre eux, il existe 2 polynôme p et p’ tels que pA +p’B = 1 (Th de BEZOUT)

ce théorème est aussi vrai pour 2 entiers relatifs premiers entre eux, A et B , p et p’ étant dans ce cas des entiers relatifs.

Corollaire évident :

Si A et B premiers entre eux et si A divise BC alors, A divise C

Division selon les puissances croissantes

A et B sont des polynômes. B est de valuation nulle (son coefficient sans X , b₀ , est non nul)

n étant un entier naturel arbitraire, a lors, il existe un couple de polynômes et un seul tel que

A = BQ + RXⁿ⁺¹ et degré de Q ≤ n

R et Q s’appellent quotient et reste d’ordre n de la division selon les puissances croissantes.

Supposons qu’on veuille diviser selon les puissances croissantes X+1 par X² +X+1 à l’ordre 4 .

On procède comme pour la division euclidienne après avoir rangé les polynômes par puissances croissantes :

Il suffit de prendre

Q = 1 – X² + X³ et R = –1

Pour avoir la relation cherchée

1 + X = (1 + X + X²)( 1 – X² + X³)+ (–1) X⁵

Remarque à l’ordre 3 on aurait eu

R = -X car -X⁵ = (–X).X⁴)

A l’ordre 2 : R = 1+X

car X³ + X⁴ = (1+X)X³.

On ne s’arrête que lorsque la valuation de RXⁿ⁺¹ est supérieure à l’ordre souhaité.

1 + X 1 + X + X²

1+ X + X² 1 – X² + X³

^– X²

-X² –X³ –X⁴

X³ + X⁴

X³ + X⁴ + X⁵

–X⁵

fonctions polynomiales

P(x) : X → a_nXⁿ + …..+a₁X + a₀ est appelée fonction polynomiale

a racine de P ⇔ P(a) = 0 ⇔ P est divisible par (X – a)

multiplicité de a racine de P : c’est le plus grand entier n tels que p soit divisible par (X – a) ⁿ

On parle de racine simple (n = 1), double (n = 2), triple (n=3) , …

● Un polynôme non nul de degré n admet au plus n racines distinctes.

● Tout polynôme non constant à coefficients dans C admet au moins une racine complexe.

● Dans C la somme des multiplicités des racines est égale au degré du polynôme.

● Quand on sait qu’un polynôme admet une racine rationnelle (p/q) , on peut quelquefois la calculer en remarquant que q divise forcément a_n et p divise forcément a₀. p–q divise P(1) et p+q divise P(–1) ce qui nous fait progresser dans la recherche d’une solution par tâtonnements.

-------------------------------------------------------------------------------------------------------------------------------------

Un calcul facile de P(a)

Dans la division euclidienne de P par (X–a), on a forcément : P = (X – a) Q + P(a)

Si a_n, …. ,a₀ sont les coefficients de P et b_n-1, ……b₀ les coefficients de Q, on a entre ces coefficients les relations suivantes :

an = bn-1 an–1 = bn–2 – abn–1 an–2 = bn–3 – abn–2 ……………………….. a0 = P(a) – ab0

bn–1 = an bn–2 = an–1 + abn–1 bn–3 = an–2 + abn–2 ……………………….. P(a) = a0 + ab0

Donc, selon le second type de correspondance, on peut de proche en proche calculer b_n–1, b_n–2 et ainsi de suite jusqu’à P(a), par de simples additions ce qui est plus facile que de calculer les puissances de a , de les multiplier par les coefficients et de les ajouter .

Dérivées et applications

Dérivées d’ordre n . On a notamment ; (PQ)⁽ⁿ⁾ =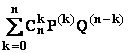

Formule de Taylor :

P = P(a) +

Peut être considérée comme l’expression de P dans une base { 1, (X–a) , (X–a)² , …, (X–a)ⁿ }

Fractions rationnelles

À partir de l’anneau des polynômes, on construit le corps R(X) des fractions rationnelles de type

où N(X)∈ R[X] et D(X) ∈ R[X] avec D(X) ≠ 0

Malgré un risque de confusion avec R[X] on note cet ensemble R(X) pour souligner qu’il est formé à partir de polynômes à coefficients réels. C(X) si les coefficients sont complexes.

Cette fois R(X) contient les polynômes et tout élément non nul est inversible . Y compris les polynômes qui n’étaient pas inversibles dans R[X] sauf quand ils étaient réduits à un entier non nul.

L’inverse de est . L’inverse de P(X) est .

● On dit qu’un nombre réel a est substituable dans une fraction rationnelle N/D si D(a) ≠ 0 ou si D(a) = 0 et N(A) = 0. Ce dernier cas permettant de simplifier la fraction par (X – a)

Quand la fraction a été simplifiée de telle sorte que N et D n’aient plus aucune racine commune, sur l’ensemble des éléments substituables dans N/D on définit l’application :

X ➜ qu’on appelle fonction rationnelle.

Les valeurs qui annulent D(X) sont appelées : Pôles de la fraction.

----------------------------------------------------------------------------------------------------------------------------------

Décomposition en éléments simples

0 Ecrivons P/Q sous une forme irréductible (Q unitaire, P et Q premiers entre eux)

1 Supposons d°(P) ≥ d°(Q)

On peut écrire de manière unique avec E et R polynômes (d°(R) <d°(Q))

Relation équivalente à P=EQ+R ou E est la partie entière et R le reste de la division euclidienne P/Q.

Si d°(P) < d°(Q) alors E = 0 et R = P .

3 Supposons d°(P) < d°(Q) (qui pourrait être le R/Q de la précédente décomposition)

Si on peut écrire D sous la forme D = D₁ D₂…D_n , ces facteurs étant unitaires et premiers entre eux deux à deux. Il existe alors des polynômes P₁, P₂ , …P_n tels que l’on puisse écrire :

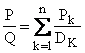
On le démontre d’abord pour n = 2 à partir de BEZOUT AD₁ + BD₂ = 1 qu’on multiplie par P/D₁D₂ pour trouver la relation cherchée (B= P₁ et A=P₂). Puis, on procède par récurrence.

4 Si dans chaque PK / DK on sépare la parie entière EK

On a 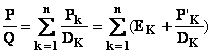avec d° (P’_k) < d°(D_k) et en réduisant au même dénominateur, on trouve que

Σ E_K est la partie entière de P/Q qu’on sait nulle puisque d°(P) < d°(Q).

avec d° (P’_k) < d°(D_k) et cette décomposition est unique

5 Si on est dans le corps des complexes, le théorème de D’Alembert nous dit qu’on peut toujours écrire Q unitaire sous la forme (X-a₁)ⁿ¹ (X-a₂)ⁿ²…..(X-a_k)^nk . Les facteurs étant unitaires et premiers 2 à 2, on peut appliquer la décomposition précédente

6 Intéressons nous à un pôle d’ordre p

d’où P = P₁Q₂ + (X–a)^p (P₂+Q₂E) avec d°(P1) < p

P₁ = quotient de la division de P par Q₂ selon les puissances croissantes de (X-a)

reste (P₂+Q₂E)

Ce quotient s’obtient après le changement de variable Y = X – a dans P et dans Q₂. En pratique, si on a affaire à un pôle d’ordre 3, il suffit de s’intéresser à la division selon les puissances croissantes de Y des 3 termes de plus bas degré de P par les 3 termes de plus bas degré de Q₂.

On trouve P₁ = b_p +b_p-1Y +…..+b₁Y^p-1 autrement dit P₁ = b_p +b_p-1(X-a) +…..+b₁(X-a)^{p-1 .}

Et enfin 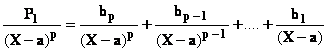où les b _i sont des constantes

7 Pour un pôle simple on a

si nous multiplions les 2 membres par (X-a) et que nous faisons X = a ,

il reste P₁ = . C’est ainsi qu’on procède pour trouver P₁. d°(P1) < 1 ⇨ P1 = constante.

8 Quand il ne reste plus que quelques valeurs, dans la décomposition quasi complète, on peut aussi donner à X des valeurs quelconques qui ne sont pas des pôles et on obtient des équations du 1^er degré dont les inconnues sont les valeurs cherchées. Il suffit de substituer X autant de fois que nous avons d’inconnues.

9 Quand nous avons besoin d’une décomposition réelle et que nous avons une décomposition complexe, il suffit d’ajouter les fractions où figurent les racines complexes d’un même polynôme (en général conjuguées) et on obtient une fraction à coefficients réels dont le dénominateur est le polynôme sans racine réelle et le numérateur un polynôme de degré inférieur.

Exemple :

Décomposer en éléments simples

R =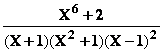

On a 2 pôles complexes (i et –i) , un pôle réel simple (–1) , un pôle réel double (1) .

R doit s’écrire R = avec A, B, C, D, E ÎC

● Si on avait un pôle triple (X-a)³ , on le décomposerait en 3 fractions, ayant pour dénominateur

(X-a)³ , (X-a)² et (X–a) .

Calcul de la partie entière E_x

On fait la division Euclidienne de X⁶ +2 par le dénominateur X⁵ –X⁴ –X +1. On trouve X + 1.

E_x = X +1

● si le degré du dénominateur de R était supérieur à celui du numérateur on aurait E_X = 0

Calcul de A

Pôle simple

On a 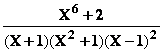= E_X + avec A constante et K polynôme.

En multipliant les 2 membres par (X+1) et en faisant X = –1 on obtient

A = valeur de 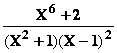pour X = –1 soit A = 3/8

Calcul de D et E

Pôle multiple

On a 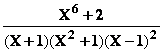= avec P et K polynômes.

Faisons le changement de variable Y = X –1 ou X = Y + 1

On obtient :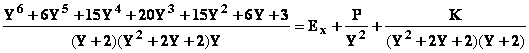

P est le quotient suivant les puissances croissantes de Y de (Y⁶+6Y⁵+…+6Y+3) par (Y²+2Y+2)(Y+2) à l’ordre 1 .

(Y²+2Y+2)(Y+2) = 4+6Y+4Y²+Y³ .

À l’ordre 1 , il est équivalent de diviser 3+6Y par 4+6Y et on trouve P = 3/4 + 3/8Y = 3/4 + 3/8(X–1),

puis en divisant par (X-1)² on identifie :

D = 3/8 et E = 3/4

Calcul de B et C

Pôles complexes

On a 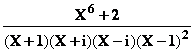= E_X +

En multipliant les 2 membres par (X+i) et en faisant X = -i on trouve :

B = valeur de 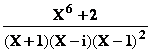quand X = – i soit (1+ i ) / 8 .

C étant la valeur conjuguée de B : B = (1 + i ) / 8 et C = (1 – i ) / 8

En conclusion

Dans =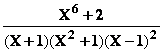

● Eventuellement, nous pouvons regrouper les fractions (2 et 3) autour des pôles complexes pour obtenir une décomposition en fractions à coefficients réels.