MATRICES

Opérations sur les matrices

Si on note a _ik le coefficient figurant à l’intersection de la i^ème ligne et de la k^ième colonne d’une matrice A ,

b _ik pour la matrice B , c _ik pour la matrice C.

Si A , B et C appartiennent à l’ensemble des matrices à n lignes et p colonnes (M _{n p} )on définit les opérations suivantes :

● addition C = A + B telle que c _ik = a _ik + b _ik

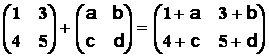
● multiplication par un scalaire C = λA telle que c _ik = λ a _ik

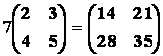
● produit d’une matrice A à p lignes et n colonnes par une matrice B à n lignes et s colonnes

Pour que AB soit défini, il faut que le nombre de colonnes de A soit égal au nombre de lignes de B

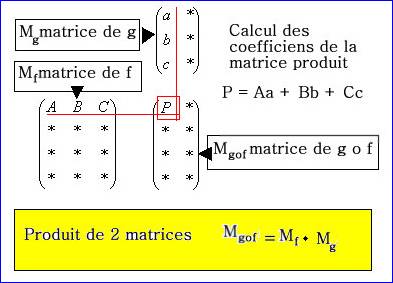
Si ( L _i ) est un vecteur ligne de A et ( C _k ) un vecteur colonne de B

Produit de matrices C = A.B tel que c _ik = ( L _i ) . ( C _k ) Produit scalaire de ( L _i ) par ( C _k )

C = AB est une matrice à p lignes (comme A) et s colonnes (comme B) .

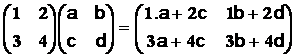
Opérations sur les matrices et applications linéaires

Si A est la matrice de f et B la matrice de g :

● La somme de 2 matrices correspond à l’application somme de 2 applis de E dans F : f + g → A + B

● Le produit d’une matrice par un scalaire λ correspond à l’application λf : λf → λA

● Le produit d’une matrice A de M _{n p} par une matrice B de M _{p s} correspond à g ○ f → A.B

Soit f une application linéaire de E dans F de matrice A

Soit g une application linéaire de F dans G de matrice B

E (dim n) f F (dim p) g G (dim s)

Alors C = A.B est la matrice de l’application g ○ f de E dans G (inversion de l’ordre d’écriture)

Matrice de l’identité dans E (I_E )

C’est une matrice carrée dont tous les coefficients sont nuls sauf ceux de la diagonale principale qui sont égaux à 1.

On peut aussi appeler I_E (ou I ) cette matrice.

Ensembles de matrices

M _{n, p} ensemble des matrices à n lignes et p colonnes

Doté de l’addition et de la multiplication par un scalaire M _{n p} est un espace vectoriel .

On en construit une base dite canonique grâce aux n.p matrices dont tous les coefficients sont nuls sauf 1 (jamais le même). Par exemple

M =

M a pour coordonnées (5, 6, 7, 8) dans la base canonique de M₂₂ qu’on appelle aussi M₂ .

M _n matrices carrées d’ordre n

C’est aussi, bien sûr un espace vectoriel mais de plus dans M _n la multiplication des matrices est

● associative, ● distributive à gauche et à droite ● et elle admet un élément neutre (I )

Mais : Elle n’est pas commutative, pour la bonne raison qu’en général g ○ f différent de f ○ g.

Matrices carrées

M _n est l’ensemble des matrices carrées (n lignes, n colonnes)

● une application f de E dans E est associée à une matrice carrée

● une application f de E dans F est associée à une matrice carrée si dim (E ) = dim (F )

● Une application bijective f est associée à une matrice carrée (réciproque fausse)

Comme f est bijective , il existe (dans ce cas seulement) une application réciproque f ^–1 elle aussi bijective Si la matrice A est associée à f , on appelle A^-1 la matrice associée à f^-1 .

On dit alors que A est inversible et que A^-1 est la matrice inverse de A .

● Calcul de la matrice inverse

V = f(v) s’écrit avec les matrices (V) = M.(v). Cela nous donne un système tel que

X₁ = x₁a₁₁ + x₂a₁₂ + …..+x_na_1n

………………………………

X_n = x₁a_n1 + x₂a_n2 + …..+x_na_nn

il suffit de le résoudre et on obtient

x₁=X₁b₁₁+X₂b₁₂+…+X_nb_1n

…………………………………

x_n=X₁b_n1+X₂b_n2+…+X_nb _nn

Le premier système qui définit f donnait les coordonnées de V en fonctions de celles de v.

Le nouveau système donne les coordonnées de v en fonction de celles de V. Il définit donc f^-1

Les coefficients b _ik de ce système forment la matrice A^-1 associée à f^-1.

● Matrice de changement de base

Soit b et B deux bases de E. Si un vecteur V a pour coordonnées V_b=( x_1, x₂, .., x_n) dans la base b il a d’autres coordonnées

V_B =( X_1, X₂, .., X_n ) dans la base B.

Le système qui permet de calculer V_B en fonction de V_b a cette allure :

X₁ = x₁a₁₁ + x₂a₁₂ + …..+x_na_1n

…………………………………

X_n = x₁a_n1 + x₂a_n2 + …..+x_na_nn

Il lui correspond donc une matrice carrée formée des coefficients a _ik qui est elle aussi inversible. Un vecteur colonne de la matrice a _ik exprime un vecteur b_i de la base b dans la base B. Ceux de la matrice inverse expriment les vecteurs de B dans la base b.

Attention, la matrice M telle que V_B = M V_b permet de calculer les coordonnées de V dans la base B quand on connaît ses coordonnées dans la base b mais on l’appelle « matrice de passage de la base B à la base b » alors que ce devrait être le contraire. C’est une bizarrerie mathématique.

« Passage de B à b » → V_B = M V_b → vecteurs colonnes b = f(B) (b_i en fonction de B)

« Passage de b à B » → V_b = M^-1 V_B → vecteurs colonnes B = f(b) (B_i en fonction de b)

● Toute matrice inversible peut être considérée comme une matrice de changement de base.

On a M.M^-1 = I où I est la matrice carrée de l’identité (coefficient de la diagonale = 1, les autres = 0)

On peut utiliser cette relation pour calculer l’inverse d’une matrice en faisant le produit de M dont les coefficients sont connus par une matrice dont les coefficients sont des inconnues, puis en identifiant les coefficients du produit aux coefficients de I.

Mais ce n’est pas la méthode la plus simple ni la plus naturelle.

● Toute matrice carrée n’est pas forcement inversible

● Matrice carrée et système de n équations à n inconnues .

Soit M une matrice carrée de M_n. J’écris (V) = M (v) , si je remplace les coordonnées de V par des nombres arbitraires, j’obtiens un système de n équations à n inconnues dont les inconnues sont les coordonnées (x₁ , x₂ , … x_n) de v . Résoudre ce système revient à trouver les coordonnées de v connaissant celles de V . Si j’y arrive, c’est que la matrice est inversible. Donc

● Soit le système admet n valeurs de x_i comme solutions et la matrice est inversible

● Soit ce n’est pas le cas et la matrice n’est pas inversible

À l’inverse, pour qu’un système admette n solutions, il faut que sa matrice soit inversible.

Soit par exemple le système 5x + 3y -4 =0 (E1) et 2x + 7y = 8 (E2) . On l’écrit sous la forme

E1 : 4 = 4x + 3y et sa matrice est 4 3 (4, 8) sont les coordonnées de V et (x, y ) celles de v

E2 : 8 = 2x + 7y 2 7

● matrices triangulaires

Je sais que je si je combine toute équation d’un système à une combinaison linéaire des autres, j’obtiens un système équivalent. Je peux utiliser cette propriété pour essayer d’annuler tous les éléments qui sont sous la diagonale principale de la matrice. Par exemple :

E1 : 4 = 4x + 3y je remplace E2 par 2.E2 – E1 j’obtiens E1 : 4 = 4x + 3y dont la matrice est 4 3

E2 : 8 = 2x + 7y E3 : 12 = 0x + 11y 0 11

Une matrice dont tous les éléments sous la diagonale sont nuls est dite « triangulaire »

Si il n’y a pas de 0 dans la diagonale d’une matrice triangulaire, la matrice est inversible et c’est aussi le cas de la matrice originelle puisque le système d’équations ainsi obtenu est équivalent au premier. Il est plus simple de calculer l’inverse d’une matrice triangulaire, mais s’il faut commencer par la triangulariser, la difficulté est à peu prés équivalente.

Modification de la matrice d’une application linéaire par un changement de base

Soit M _{b B} la matrice de f application linéaire de E rapporté à une base b dans F rapporté à une base B.

● Si on change soit la base b pour b’ , soit la base B pour B’ (ou les 2 à la fois), l’application linéaire continue à exister mais sa matrice change de forme. Elle a toujours n lignes et p colonnes mais ses coefficients ne sont pas les mêmes. Par exemple, on va appeler la nouvelle matrice M _{b B’ .}

● On peut appeler B _{b b’} la matrice du changement de base b → b’ qu’on appelle C _b

et B _{B B’} celle du changement de base B → B’ qu’on appelle C _{B .}

● de la même façon, on peut appeler f _{b B} l’application quand elle est définie dans les bases b et B

f _{b B’} l’application quand elle est définie dans les bases b et B’

● on peut considérer que f _{b B’} est la composition de f _{b B} suivie du changement de base dans F : C _B.

E _b F_B F_B’

v_b f _bB V_B C_B V_B’

v_b f _bB’ V_B’

f _{b B’} = C _B ○ f _{b B} .

On en déduit que M _{b B’} = M _{b B} . B _{B B’} si le changement de base à lieu dans F

Et si le changement de base à lieu dans E : M _{b’ B} = B^–1_bb’. M _{b B} ou B _b’b . M _bB

Il faut d’abord faire le changement de base b’ → b qui est le changement réciproque de b → b’ avant de pouvoir appliquer f _{b B} qui est définie dans la base b .

Si les deux changements de base, dans E et dans F sont simultanés M _{b’ B’} = B^–1_bb’. M _{b B .} B _{B B’ .}

(En rouge l’ancienne matrice de f , en bleu la matrice de f après changement de base, en noir les matrices de changements de base)

Deux matrices M et M’ sont dites équivalentes si il existe 2 matrices inversibles A et B telles que M’=AMB

C’est donc le cas de M _{b’ B} et M _{b B}

Si M et M’ sont 2 matrices carrées de M _n liées à la même application mais dans 2 bases différentes, si on appelle B la matrice de changement de base on aura M’ = B^–1MB et les matrices seront dites semblables.

Vecteurs propres, valeurs propres

Soit f une application linéaire dans E . Sa matrice est carrée et appartient à M _n.

Si il existe des vecteurs x non nuls colinéaires à leur image c'est-à-dire tels que f(x) = λx (λ Î R ) on les appelle des vecteurs propres. Dans ce cas, tout vecteur colinéaire à x est un vecteur propre, mais λ est unique pour les vecteurs du sous espace engendré par {x} car si f(kx) = kλ’x = kf(x) = kλx on a forcément λ’=λ. λ est appelé valeur propre associée au vecteur propre x (et à toute sa famille) .

Si il existe une base b de E formée de n vecteurs propres {b_i} chacun étant associé à une valeur propre λ_i .

Alors, on a pour tout vecteur de la base f ( b _i ) = λ _i . b _i et la matrice de f dans cette base s’écrit par exemple:

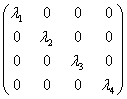
La diagonale principale est formée des valeurs propres et les autres coefficients sont nuls. Une telle matrice est dite « diagonale ».

Une matrice pouvant être transformée en une matrice diagonale par un changement de base est dite « diagonalisable ».

Par exemple, la matrice d’une rotation d’angle π est diagonalisable, puisque f(x) = – x .

Opérations élémentaires sur les matrices

Le rang de f est la dimension de Im (f) . C’est aussi le rang de la matrice M associée à f. Et aussi le rang du système de vecteurs lignes ou colonnes de la matrice. (combien sont linéairement indépendants ?)

On appelle opérations élémentaires sur M

1) la permutation de 2 lignes (resp. colonnes) ce qui revient à inverser l’ordre des vecteurs d’une base

2) l’ajout à une ligne (resp. colonne) d’une combinaison linéaire d’autres lignes (resp. colonnes) , ce qui revient à remplacer un vecteur d’une base par un vecteur qui reste indépendant des autres.

3) La multiplication d’une ligne (resp. colonne) par un scalaire λ non nul ce qui revient à diviser par λ un vecteur d’une base.

En fait, les opérations élémentaires reviennent à modifier partiellement une base et la remplacer par une autre. Les opérations élémentaires sur M transforment M en une matrice M’ de même rang.

Et deux matrices de même rang sont équivalentes. (La réciproque est vraie) .

Donc, quand on procède à une opération élémentaire sur M, on obtient une nouvelle matrice M’ qui peut être considérée comme liée à l’application f si on choisit convenablement la base b’ de E et la base B’ de F.

Retour sur les applications linéaires

Soit f application linéaire de E de dimension n dans F de dimension p .

Ker (f ) est un sous espace vectoriel de E de dimension r .

Donc E est égal à la réunion de 2 SEV disjoints Ker (f) et son supplémentaire qu’on appellera G.

● G est un SEV de dimension n – r qui admet comme base { b ₁,……,b _{n– r} }

Ker (f ) est un sous espace vectoriel de dimension r qui admet comme base { b _{n – r + 1} , ……., b _n }

Et la réunion de ces 2 bases B = { b ₁ , …….. , b _n } forme une base de E .

● les images des vecteurs de la base de G forment un système libre de n – r vecteurs dans F .

En effet, s’il existait des scalaires λ _i non tous nuls, tels que λ₁ f( b ₁) + ……+ λ _{n – r} f (b _{n– r} )= 0

On aurait f( λ₁b ₁ + ……+ λ _{n – r} b _{n– r} ) = 0 et λ₁b ₁ + ……+ λ _{n – r} b _{n– r} appartiendrait au noyau ker ( f ) ce qui est incompatible avec nos hypothèses (ce vecteur appartient au supplémentaire du noyau) .

● On en déduit au passage que la restriction de f à G supplémentaire de Ker ( f ) est injective.

● Donc { f ( b ₁ ), …….. , f ( b _{n –} r ) } système de vecteurs linéairement indépendants de F peut être complétée par p – ( n – r ) vecteurs de F choisis pour former une base de F. Appelons B’ cette base de F .

● Si on prend un vecteur de la base B , son image par f s’écrira dans la base B ‘ :

Pour i ≤ n – r : f (b _i ) = ( 0, 0, ….., 0 , 1 , 0 , …..0) seule sa i^ème coordonnée n’est pas nulle

Pour i > n – r : f ( b _i ) = (0 , …………………….., 0) puisque b _i appartient au noyau .

● Donc, si on choisit B comme base de E et B’ comme base de F , la matrice de f s’écrira par exemple :

M =

De cette écriture on déduit

● que Im ( f ) est de dimension 4 donc que la matrice et f sont de rang 4 (quatre 1 dans la diagonale) .

● Que Ker ( f) est de dimension 2 (2 colonnes de 0 )

● Que l’application n’est pas surjective (une ligne de 0 ) et que

Dim F = Dim (Im ( f ) ) + 1

● Soit une autre application linéaire de rang 4 de E dans F , on va pouvoir par le même procédé, la transcrire en une matrice égale à M (mais dans d’autres bases) . C’est donc que 2 matrices de même rang sont équivalentes.

● Si une matrice 5 x 6 telle que M est de rang 4 , c’est que je peux annuler 2 des ses vecteurs colonnes et un de ses vecteurs lignes en leur ajoutant une combinaison linéaire des autres et par d’autres opération élémentaires obtenir une matrice semblable à M

● Si l’application est bijective, en choisissant les bases B et B’ selon le même procédé, on peut l’écrire sous la forme d’une matrice carrée dont la diagonale est formée de 1 , les autres coefficients étant nuls.

Mais s’agissant d’une application de E dans F il ne faut pas la confondre avec l’identité.

Par exemple pour une rotation dans le plan :

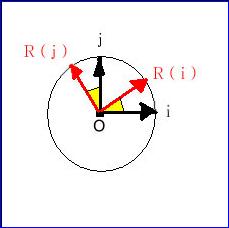Si le plan de départ et le plan d’arrivée sont rapportés à la base {i , j}, la matrice de la rotation est

Mais si on garde {i , j } pour le plan de départ et on pend {R ( i), R (j)} pour le plan d’arrivée la matrice de la rotation devient

Si on modifie l’ordre de la base d’arrivée {R (j) , R(i)} la matrice devient : (Permutation des vecteurs lignes)

Si je prends pour base d’arrivée {R (j) , } la matrice devient (multiplication de la ligne 2 par λ)

Et ainsi de suite, on peut retrouver sur cet exemple tous les changements de base correspondant aux opérations élémentaires sur les matrices.

Dans tous les cas, si on garde la base de départ { i , j } la première colonne sera R ( i) et la seconde R (j) puisque ce sont les images de la base de départ par R, mais les coordonnées de R ( i ) et de R (j) changeront selon le choix de la base d’arrivée.

Une modification sur les lignes impacte la base de F, une modification sur les colonnes, la base de E.