LIMITES et CONTINUITE

Quelques notions de topologie.

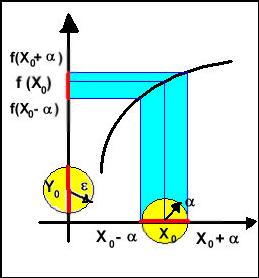
Dans ce qui suit nous considérons que f est une fonction quelconque.

Nous dessinons le graphe de cette fonction et nous choisissons un point x₀ sur l’axe des x dans le domaine de définition.

Nous traçons le cercle de centre x₀ et de rayon ⍺ qui coupe l’axe des x en x₀ – ⍺ et x₀ + ⍺.

Nous traçons aussi le cercle de centre y₀ (y₀ arbitraire sur l’axe des y) et de rayon ε qui coupe l’axe des y en y₀ – ε et y₀ + ε.

Une boule fermée de rayon a (toujours positif) centrée sur x₀, est notée B(x₀ , ⍺).

Dans R c’est l’intervalle [x₀ – ⍺ ; x₀ + ⍺ ]

Si la boule était ouverte ce serait l’intervalle ] x₀ – ⍺ ; x₀ + ⍺ [.

De la même façon, on peut définir

une boule dans R² comme un disque de centre (x₀ , y₀)

et une boule dansR³ comme une sphère de centre (x₀ , y₀ , z₀).

La boule est dite ouverte ou fermée selon qu’elle contient ou non sa frontière (les bornes de l’intervalle, la circonférence du disque ou l’enveloppe de la sphère).

Les bornes de l’intervalle [x₀ – ⍺ ;x₀ + ⍺ ] constituent un encadrement de x₀ puisqu’on a x₀ – ⍺ < x₀ < x₀ + ⍺.

Un boule constitue un voisinage du point situé en son centre. Qu’est ce qu’un voisinage de x₀ ? C’est un ensemble contenant une boule ouverte contenant x₀. Dans R, n’importe quel intervalle contenant x₀ constitue un voisinage de x₀. L’intérêt de choisir une boule et pas n’importe quel voisinage, c’est qu’en faisant varier le rayon de la boule (ici ⍺) , on va pouvoir suggérer par exemple qu’on se rapproche de x₀ autant qu’on le désire quand le rayon rétrécit (quand ⍺ diminue) .

Comment traduire le fait que x, un réel quelconque appartient à la boule ouverte B(x₀,a) ?

x ∈ B(x₀ , ⍺) équivaut à | x₀ – x| < ⍺ , sur la droite R , la valeur absolue de x₀ – x est aussi la distance de x₀ à x (d(x₀,x)) et cette distance est inférieure au rayon de la boule qui est ⍺. d(x₀,x) < ⍺.

Evidemment, Sur l’axe des y, les mêmes notions ont cours : la boule ouverte de centre y₁ et de rayon ε est l’intervalle ] y₀ – ε ; y₀+ ε [ et elle constitue un voisinage de y₀. Il est équivalent d’écrire

f(x)∈ B(y₀, ε ) ou | y₀ – f(x)|< ε ou , si y₀ = f(x₀) : d(f(x₀), f(x)) < ε

Image d’une boule par f.

Dans notre exemple, la fonction étant continue et monotone (toujours croissante) pour x ∈ B(x₀ , ⍺) on peut dire que l’image de B est l’intervalle ]f(x₀ – ⍺) ; f(x₀ +⍺)[ . Mais ça ne sera pas toujours le cas (imaginez que f admette un maximum en x₀) . En règle générale, l’image d’une boule ouverte n’est pas une boule, c’est un intervalle ou une réunion d’intervalles de l’axe des y, qui peuvent être ouverts ou fermés selon que la fonction est monotone ou non, continue ou non sur la boule.

Image réciproque d’une boule

Ici, si on cherche l’image réciproque de B(f(x₀₎ , ε) ce n’est pas non plus forcément une boule. En règle générale c’est un intervalle de l’axe des x ou une réunion d’intervalles, mais tout dépend du rayon de la boule, de la continuité ou de la monotonie de la fonction.

Imaginer l’image d’une boule ou l’image réciproque d’une boule en fonction des particularités du graphe et du rayon des boules, est un exercice capital pour la compréhension des notions qui vont suivre.

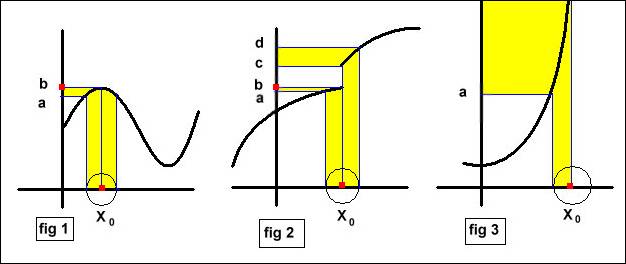
En guise d’exercice remplacez le graphe de f dans le dessin de notre exemple par  les graphes ci dessous :

Cherchez l’image de B(x₀, ⍺) L’image réciproque d’une boule B(y₁,ε) et faites varier le rayon des boules.

--------------------------------------------------------------------------------------------------------------------------------------

Limite finie de f(x) quand x tend vers x₀ , valeur finie

Supposons que cette limite L existe. On note

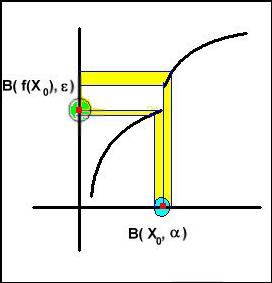
● cette limite L existe si et seulement si, aussi petit que nous choisissions le rayon ε de la boule B(L, ε) centrée sur L (axe des y ) il existe une boule B (x₀ , ⍺) centrée sur x₀ (axe des x) dont l’image est toute entière à l’intérieur de B(L,ε) .

Dans notre dessin, quel que soit le choix de L sur l’axe des y, cette condition n’est pas réalisée. En effet l’image de la boule bleue (projetée en jaune) qui est la réunion de 2 intervalles disjoints ne peut être contenue dans la boule verte si on choisit son rayon ε assez petit.

La limite de f en X₀ n’existe pas.

● Une condition équivalente : si et seulement si :

◙ tout ε > 0 , $ ⍺ > 0 | |x₀ – x| < ⍺ ⇒ |f(x) – L| < ε (ce qui équivaut à f(B(x₀, ⍺)) ⊂ B(f(x₀) , ε) )

◙ Tout ε positif , il existe ⍺ positif tel que

le choix de x dans l’intervalle ] x₀-⍺ ; x₀+⍺[ implique que

f(x) se trouve dans l’intervalle ] L -ε ; L+ε[

◙ Tout ε positif, il existe ⍺ positif tel que pour tout x, d(x , x0) < ⍺ implique d(f(x), L) < ε .

● Si la limite de f(x) en x = 0 est 0 (le graphe passe par l’origine)

La condition tout (∀) ε > 0 , il existe (∃) ⍺ > 0 | |x₀ – x| < ⍺ ⇨ |f(x) – L| < ε devient

∀ ε > 0 , ∃ ⍺ > 0 | |x| < ⍺ ⇨ |f(x)| < ε (il suffit de faire x₀ = 0 et L = 0 dans la formule précédente)

● pour appliquer ces critères, il faut que le domaine de définition de f (Df) contienne un intervalle

] x₀-⍺ ; x₀+⍺[ . Même si la valeur x₀ est exclue du domaine de définition.

Par exemple pour x₀ = 0 , les deux fonctions suivantes ne sont pas définies mais:

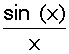admet pour limite 1 , n’admet pas de limite

● limite à gauche (à droite)

On garde la boule de rayon e autour de L mais elle doit contenir l’image d’une demie – boule autour de x₀. existe si

∀ ε > 0 , ∃ ⍺ > 0 | x₀ – x < ⍺ ⇨ |f(x) – L| < ε

Plus de valeur absolue autour de |x₀ – x|. Pour une limite à droite, on remplacerait x₀ – x par x – x₀.

● L’existence d’une limite L de f(x) pour x ➜ x₀ suppose l’existence d’une limite à droite et à gauche et leur égalité à L.

● Théorème des gendarmes : si il existe un voisinage de x₀ au sein duquel on a

g(x) ≤ f(x) ≤ h(x) et que g(x) = h(x) = L alors on peut dire que f(x) = L

Par exemple, on a et on en tire la conséquence que

● Si f(x₀) existe , alors = f(x₀)

● On dit qu’une fonction f(x) est continue en x = x₀ ∈ Df si f(x₀) existe et

● Si la fonction n’est pas définie au seul point x₀ mais qu’elle admet une limite L en ce point, on dit qu’on la prolonge en continuité en posant

f(x₀) = L .

Par exemple, on peut prolonger f(x) = ou f(x)= en continuité en posant f(0) = 1.

Limites infinies de f(x) quand x tend vers une valeur finie

Quand on écrit, il s’agit en fait d’un abus de langage.

On devrait dire « f(x) tend vers +∞ quand x tend vers x_0 » car l’infini n’est pas vraiment ce qu’on peut appeler « une limite ». Cette fois, l’image d’une boule ouverte B (x₀ , ⍺) centrée sur x₀ doit être un intervalle de la forme ] A, +∞ [ et plus le rayon ⍺ de la boule diminue, plus A doit devenir grand, sans limite. Ce qu’on traduit par

si et seulement si ∀ A , ∃ ⍺ > 0 | |x₀ – x| < ⍺ ⇨ f(x) > A

si et seulement si ∀ A , ∃ ⍺ > 0 | |x₀ – x| < ⍺ ⇨ f(x) < A

Pour les limites à gauche (resp. à droite) il faut remplacer |x₀ – x| par x₀ –x (resp. x–x₀)

Dans ces cas de figures, on dit que le graphe admet une asymptote verticale.

En voici 2 cas :

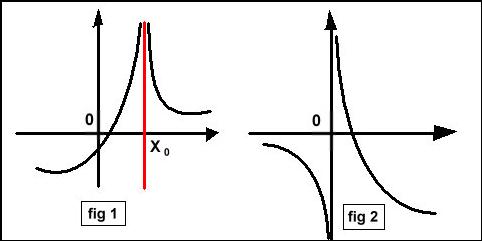fig 1 :

quand X ➜ X₀ on peut dire que

f(x )➜ +∞

fig 2

Quand X ➜ 0

f(x) n’a pas de limite infinie

mais une limite à gauche

f(x) ➜ – ∞

et une limite différente à droite

f(x) ➜ +∞

Les asymptotes verticales sont respectivement la droite X = X₀ et X = 0 .

Limites de f(x) quand x tend vers –∞ et +∞

● Quand x et f(x) tendent tous vers + ou - ∞ , il y a plusieurs cas de figures

X →	lim (fx) = +∞	lim (fx) = –∞
+∞	∀ A , ∃ B | x > B ⇨ f(x) > A	∀ A , ∃ B | x > B ⇨ f(x) < A
–∞	∀ A , ∃ B | x < B ⇨ f(x) > A	∀ A , ∃ B | x < B ⇨ f(x) < A

Au sein de chaque configuration on distingue encore 2 cas

◙ f (x) → vers l’infini en se rapprochant d’une droite oblique d’équation y = ax+b.

Alors, on dit qu’il y a une asymptote oblique.

On doit trouver que .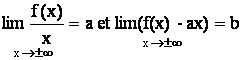

◙ dans le cas contraire, il n’y a pas d’asymptote mais une branche infinie

● Quand x → ±¥ et que f(x) → a, valeur finie. On dit qu’il y a une asymptote horizontale

X ➜	lim (fx) = a
+∞	∀ ε>0 , ∃ B | x > B ⇨ |f(x) – a| < ε
–∞	∀ ε>0 , ∃ B | x < B ⇨ |f(x) – a| < ε

Dans ce cas, l’asymptote horizontale est la droite d’équation y = a .

● Quand il y a une asymptote oblique ou horizontale, pour savoir si la courbe se situe en dessus ou en dessous de la droite, il faut étudier le signe de [f(x) – équation de la droite]

quand x➜±∞. Asymptote oblique :il faut étudier le signe de f(x) – (ax + b) ou asymptote horizontale le signe de f(x) – a

REGLES DE CALCUL DES LIMITES

Limite d’un produit

Comment se comporte le produit P= AB selon que A et B tendent vers une limite

nulle, finie (L ou L’≠ 0) ou infinie ±∞ ?

On distingue les cas de limite finie nulle et limite finie non nulle (L ou L’) car selon le cas, la règle peut changer.

On étudie tous les cas de limite de P = AB dans un tableau selon les valeurs des limites de A et de B.

B	A	0	L	+∞	–∞
0		P➜0	P➜0	?	?
L’		P➜0	P➜LL’	P➜±∞	P➜±∞
+∞		?	P➜±∞	P➜+∞	P➜–∞
–∞		?	P➜±∞	P➜–∞	P➜+∞

Il n’y a finalement qu’un seul cas d’indétermination ( ?) : quand l’un des facteurs tend vers 0 et l’autre vers ±∞

(A et B « tirent en sens contraire » dans le produit)

Dans ce cas, tout dépend de l’ordre de grandeur de A par rapport à B.

La limite peut être selon le cas finie, nulle , ou ±∞

Quand on indique que P➜±∞ , le signe de P dépend en fait du signe de L ou L’.

Pour le déterminer, il suffit d’appliquer la règle des signes. Ce n’est donc pas un cas d’indétermination.

Exemples

3x² = +∞ (+(3) par + par + = +) ,

3x² =+∞ (+(3) par – par – = + )

Mais

–3x² = –∞ (– (3) par + par + = − ) ,

–3x³ = +∞ (–(3) par – par – par – = +)

On appliquerait aussi cette règle pour par exemple

[f(x).g(x)] avec f(x)= –3 et g(x) =±∞ .

Limite d’une somme

Comment se comporte la somme S = A+B selon que A et B tendent vers une limite

finie (L ou L’ ou 0 ) ou infinie ±∞ ?

La limite finie L (ou L’) peut être nulle sans que la règle soit modifiée (ce qui n’est pas le cas pour le produit).

B	A	L	+∞	–∞
L’		S➜L+L’	S➜+∞	S➜–∞
+∞		S➜+∞	S➜+∞	?
–∞		S➜–∞	?	S➜–∞

Il n’y a qu’un seul cas d’indétermination : Quand certains termes de la somme tendent vers +∞ et d’autres vers –∞

(A et B « tirent en sens contraire » dans la somme.)

Dans ce cas, tout dépend de l’ordre de grandeur de A par rapport à B.

La limite sera, le plus souvent +∞ ou –∞ (rarement un nombre fini).

Exemple

(x² + x) .

On est dans un cas d’indétermination car

x² = +∞ et x = –∞ .

Mais l’ordre de grandeur de x² est supérieur à celui de x et on va avoir

(x² + x) = +∞ .

On en fera la démonstration ultérieurement.

Par contre

(x² + x) n’est pas indéterminée car (+∞) + (+∞) = +∞

Limite d’un quotient

Comment se comporte le quotient Q = selon que A et B tendent vers une limite nulle, finie (L ou L’≠ 0) ou infinie ±∞ ?

On peut considérer que Q est le produit de A par et se référer à la règle du produit.

Pour la règle est la suivante :

B	0	L	+∞	–∞
	±∞		0	0

Si B ➜ 0⁺ (B➜0 avec B>0 limite à droite) l’inverse de B est positif, donc il tend vers +∞ .

Si B ➜ 0^– (B➜0 avec B<0 limite à gauche) l’inverse de B est négatif donc il tend vers –∞ .

Pour Q , quotient de A par B , on obtient le tableau suivant

B	A	0	L	+∞	–∞
0		?	±∞	±∞	±∞
L’		0	L/L’	±∞	±∞
+∞		0	0	?	?
–∞		0	0	?	?

Les cas d’indétermination se produisent quand numérateur et dénominateur « tirent en sens contraire ».

L’un tend à ramener Q vers zéro et l’autre vers ±∞.

C’est le cas pour

Limite d’un polynôme quand x ➜ ±∞

Quel que soit le polynôme, on peut mettre son terme de plus haut degré en facteur de la façon suivante, illustrée pour le degré 2 :

p(x) = ax² + bx + c = ax² (1 + ) .

Quand x va tendre vers l’infini, les termes comportant x au dénominateur vont tendre vers 0.

Si bien que (1 + ) = 1 . D’où on déduit que

P(x) = ax² .

Le même procédé appliqué à un polynôme de degré n permet de démontrer le résultat suivant :

Très important :

Quand X ➜±∞ , un polynôme a_nXⁿ + a_n–1X^n–1+… + a₀X⁰ se comporte comme son terme de plus haut degré a_nXⁿ

Cela permet de lever certaines indéterminations telles que

(x² + x) (on se trouve dans le cas +∞ + ( –∞) ) = x² = +∞

Limite d’un quotient de polynômes quand x ➜ ±∞

Du résultat précédent (limite d’un polynôme) on déduit :

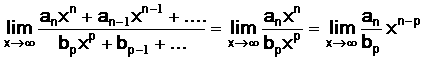
Exemples

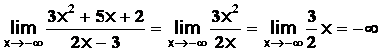
En somme on a

● si degré de D = degré de N : lim Q = a nombre non nul

● si degré de D > degré de N : lim Q = 0

● si degré de D < degré de N : lim Q = ±∞

Limite d’un quotient de polynômes quand x ➜ a

(qui annule le dénominateur)

Rappelons que

Pour que f(x) ait une limite quand x ➜a , il faut que  :

limite à gauche = limite droite.

● On factorise autant que possible le numérateur et le dénominateur de f(x) .

● Cas d’un facteur commun au numérateur et au dénominateur

Si on trouve par exemple f(x)=.

f(x) n’est pas définie pour x= –3 mais on peut écrire après simplifications par (x+3) que .

La limite est indépendante de la façon dont x tend vers –3 .

● Cas sans facteur commun au numérateur et au dénominateur

Mais si f(x) = . La fonction n’est toujours pas définie pour x = –3

● si l’on pose A(x) = f(x) dont on a exclu le facteur (x+3)

Au voisinage de x = −3 , f (x) va se comporter comme ou

selon que (x+3) va tendre vers 0 par valeur positive ou négative.

Au voisinage de x = −3 

A (x) =

● Donc quand x➜–3 , A(x) est positif et de signe stable (7/2 est positif)).

● Tandis que (x+3) va être voisin de 0 mais en changeant de signe selon que x < –3 ou x > –3, ce qui va faire basculer la limite de f(x) de –∞ à +∞ .

l Limite à gauche :

Si x < –3 alors (x+3) négatif donc = –∞

(signe de 7/2 divisé par x+3 = – )

● Limite à droite :

Si x > –3 alors (x+3) positif donc = +∞

(signe de 7/2 divisé par x+3 = + )

● Les 2 limites, (à gauche et à droite) étant différentes, on ne peut pas dire que f(x) a une limite

pour x➜ –3.

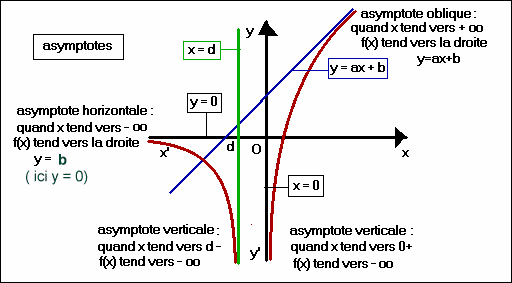
Asymptotes

On parle d’asymptote quand la courbe tend à se rapprocher indéfiniment d’une droite, sans l’intercepter.

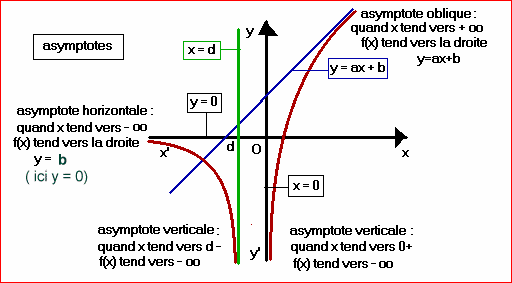
asymptote horizontale : y ➜ a quand x ➜±∞

(exemple f(x) = 1/x : ➜ 0 quand x ➜ ±∞)

asymptote verticale : y➜ ±∞ quand x ➜ a (a⁺ ou a^–)

(exemple f(x) = 1/x : ➜ ±∞ quand x ➜ 0 )

asymptote oblique : y ➜ ±∞ quand x➜ ±∞ mais il existe a et b réels tels que

[ y – (ax+b)] è 0 quand x ➜ ±∞

Test : si il existe une asymptote oblique d’équation y =ax + b

Calcul de b: une fois a calculé par le test précédent

Branche infinie : y➜ ±∞ quand x➜±∞ mais il n’y a pas d’asymptote oblique

(par exemple f(x) = x²)

Positions relatives de 2 graphes en x = x0.

Il arrive qu’on se pose la question de savoir si la courbe graphe de f(x) est située au dessus ou au dessous d’une droite d’équation

y = ax + b (ou y = b) ou plus généralement du graphe d’une autre fonction g(x).

Pour x donné

f(x) est au dessus de g(x) si f(x) – g(x) > 0

f(x) est au dessous de g(x) si f(x) – g(x) < 0

En effet, par exemple f(x) > g(x) s’écrit aussi si f(x) – g(x) > 0

Pour savoir si le graphe de f(x) est au dessus ou au dessous d’une asymptote horizontale ou oblique quand x tend vers ±∞ , on raisonne de la même façon et on étudie le signe de lim [f(x) – g(x)] quand x ➜ ±∞ (g(x) étant l’équation de l’asymptote) .

Composition des limites

Si

f(x) a pour limite L quand x ➜ a

g(x) a pour limite L’ quand x ➜ L

Alors

g ○ f (x) a pour limite L’ quand x➜ a

Domaines de définition :

Df doit contenir un voisinage de a et Dg un voisinage de L

Théorème non généralisable aux limites à droite ou à gauche.

Pratiquement, ce théorème est utile pour déterminer les limites des fonctions déduites des fonctions usuelles par un changement de variable.

Par exemple si on nous demande la limite de quand x ➜ +∞ , on peut poser U = ,

dire que la limite de U quand x ➜+∞ est 0 et donc que la limite cherchée est celle de e^U quand U ➜ 0 soit 1 .

Minorer ou majorer une fonction par une autre

À rapprocher du théorème des gendarmes .

● Au voisinage de x = a si f < g alors lim f ≤ lim g

● Au voisinage de x = a si f < g et lim f = +∞ alors lim g = +∞

on peut trouver d’autres théorèmes de ce type : par exemple si f et g positives , f < g et lim g = 0 alors, lim f = 0 .

Suites

Ce type de résultat peut être transposé aux suites qu’on peut souvent considérer comme la restriction de fonctions à N . Par exemple si U_n = 2n + 1 on peut considérer que c’est la restriction à N de f : x ➜ 2x + 1 .

La convergence de suites monotones est souvent liée à leur bornage. Par exemple :

Si U_n est une suite croissante

Soit elle est majorée et elle converge vers sup (U_n )

Soit elle n’est pas majorée et elle diverge vers + ∞

Quelques limites à connaître

On étudie d'abord ln x à partir de sa définition (aire algébrique) et de sa dérivée 1/x:

La fonction ln x n'est définie que pour x > 0 à cause de la discontinuité du graphe de 1/t pour t = 0 . (l'aire située sous la courbe y = 1/t n'a plus aucun sens quand t devient £ 0).

La dérivée 1/x est toujours positive pour x > 0 donc

ln x est strictement croissante .

On a ln 1 = 0 (aire entre t=1 et t=1)

ln x > 0 pour x > 1 et quand x➜+∞ , ln x ➜ +∞

(l'aire comprise entre t=1 et t=x est positive quand x > 1 et devient infinie quand x devient infini) .

ln x < 0 pour x < 1 et quand x ➜0⁺ , ln x → -∞

(aire négative et devenant infinie quand x tend vers 0) .

Log_ax est déduite de ln x par division par la constante ln a qui peut être plus grande ou plus petite que 1 et même négative quand a est entre 0 et 1 (courbe décroissante) .

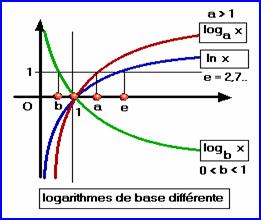
Comparer ln x , a^x , x^⍺ pour ⍺ > 0 et a >1 (e entre dans ce cas)

en +∞ les 3 fonctions tendent vers +∞ ; donc on compare leurs quotients (somme et produits sont déterminés)

l'ordre de croissance est ln x < x^⍺ < a^x donc les quotients tendent vers 0 quand x→+∞

en 0⁺ , a^x = 1 est hors circuit . x^⍺ ➜ 0 et ln x ➜ -∞. Somme et quotient sont déterminés . Reste le produit .

x^⍺ qui tend vers 0 l'emporte sur ln x qui tend vers -∞ , donc x^⍺.ln x tend vers 0 quand x➜0+ .

en -¥ , ln x n'est pas définie . a^x→ 0 et |x|^a → +∞ . Là encore , seul le produit est indéterminé .

a^x tend vers 0 plus vite que |x|^⍺ ne tend vers +∞ , donc |x|^a.a^x tend vers 0 quand x → -∞ .

CONTINUITE

Fonction continue en a si et seulement si

● f(a) existe (a Î Df) ●

Fonction continue à droite pour x ≥ a (ou à gauche pour x ≤ a )

Si La limite à droite de f(x) existe et est égale à f(a)

Fonction continue sur un sous ensemble I de Df

Si f(x) est définie et continue en tout point de I (le plus souvent un intervalle)

Fonction continue

Si elle est continue en tout point de Df

L’exemple des fonctions définies par morceaux.

● on fait une partition de R en intervalles disjoints par exemple (–∞ , -2[ U [-2 ; +3[ U [+3 ; +∞ )

● Et sur chaque intervalle, on définit f(x) différemment

E(x) = partie entière de x est assimilable à une fonction définie par morceau.

Autre exemple f(x) = x sur (–∞ , 1[ et f(x) = x+1 sur [ 1 ; +∞)

f(x) est donc définie sur R . Pour x = 1 ; f(x) est égale à x + 1 soit f(1) = 2.

Le graphe de cette fonction est le suivant :

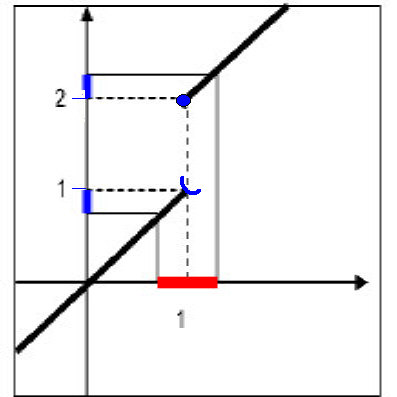
Il faut exclure le point (1,1) de la demi droite inférieure et rattacher le point (1,2) à la demi droite supérieure.

L’image d’une boule ouverte centrée sur 1 (en rouge) est une réunion d’intervalles disjoints (en bleu). Si le rayon de la boule est ⍺ , ces intervalles sont

] 1–⍺ , 1[ U [ 2 , 2+ ⍺ [ .

Quel que soit ⍺, pour contenir la totalité de cet intervalle, il faut une boule de rayon supérieur à 1. Donc si je choisis une boule de rayon 0,5 centrée n’importe où, elle ne pourra jamais contenir la totalité de cet intervalle et f(x) n’admet pas de limite pour x = 1.

Mais f(x) admet une limite à gauche (1) et à droite (2) .

Conclusion : la fonction n’est pas continue en x = 1 (le graphe en témoigne), elle est continue à droite car à droite lim f(x) = f(1) = 2 mais pas à gauche car à gauche lim (fx) = 1 différent de f(1).

● La plupart des fonctions usuelles (polynômes, sin x, ln (x), e^x, …) sont continues. Les fractions rationnelles N(x) / D(x) le sont aussi car on a exclu les valeurs qui annulent le dénominateur du domaine de définition.

Prolongement en continuité

Si f n’est pas définie en a mais que on prolonge la fonction en continuité par f(a) = b.

On en a vu un exemple pour x / x, prolongée en 0 par 1. peut être prolongée en 0 par 0

Théorème des valeurs intermédiaires

Si f est continue sur l’intervalle [ a , b ], pour tout y de l’intervalle [ f(a) , f(b)] , il existe au moins un x entre a et b tel que f(x) = y. Attention : la réciproque n’est pas vraie .

Pour notre fonction définie par morceaux, on voit bien que si x ∈ [1 -⍺ , 1 +⍺], l’intervalle [ f(a) , f(b] est [ 1 - ⍺ , 2+⍺] qui contient 1,5. mais 1,5 n’a pas d’antécédent par f. Donc f n’est pas continue.

Combinaisons de fonctions continues

Soient f et g définies et continues sur un intervalle [ a , b]

● f + g est continue sur [ a , b]

● λ

.

f est continue sur [ a , b]

● f g est continue sur [ a , b]

● f / g est continue sur [ a , b] privé des points qui annulent g

● si l’image de [ a , b] par f est E et que g est continue sur E alors g ○ f est continue sur [ a , b]

C’est grâce à ces propriétés qu’on démontre la continuité de la plupart des fonctions à partir de la continuité des fonctions usuelles, considérée comme admise.

Image d’un intervalle

Soit f une fonction définie et continue sur [ a , b ]

● si la fonction est monotone sur cet intervalle, f ([ a , b ] ) = [f(a) , f(b)] (fonction croissante) ou

f ([ a , b ] ) = [f(b) , f(a)] (fonction décroissante)

● si la fonction n’est pas monotone (elle admet au moins un maximum ou un minimum sur [a , b]) les bornes de l’intervalle image seront, selon le cas, parmi les nombres suivants

{ f(a) , f(b), Max (f(x)) , Min (f(x)) } .Exclusivement .

● Dans tous les cas, la fonction est majorée et minorée.

● Dans tous les cas, l’image d’un intervalle est un intervalle mais l’image d’un ouvert (ou fermé) n’est pas forcément l’image d’un ouvert (ou fermé). Sauf dans le cas des fonctions monotones.

Il y a des cas particuliers tels que tan (x) , l’image de ]–π/ , + π/2[ est R

ou e^x (l’image de R^– est ]0 , 1])

qui nous obligent à considérer R ou R^– comme un intervalle.

Bijections continues

Voici 3 assertions

● f est continue sur [ a, b ]

● f est monotone sur [ a, b ]

● f est bijective sur [ a, b ]

Quand deux d’entre elles sont vraies, la 3^e l’est aussi.

● Si f est bijective sur [ a, b ] , alors f^–1 définie soit sur [f(a) , f(b)] , soit sur [f(b) , f(a)] existe et c’est aussi une fonction continue.

C’est le cas de Arc sin , Arc cos, Arc tan fonction réciproques de sin , cos , tan ou de e^x réciproque de ln x .