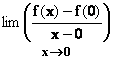LES DERIVEES ET LEURS APPLICATIONS
1 Soit M (x0 , f(x0)
) , un point fixe de la courbe d’équation y = f(x)
Et P (x ,
f(x)) un point mobile de la même courbe, distinct de M.
La droite (MP) est dite
« sécante à la courbe » , son équation est y
= ax + b et a , son coefficient directeur
est égal au taux de variation de f entre
x0 et x : a = ![]() .
.
2 Lorsque le point P se rapproche de M : x → x0 , f(x) → f(x0) donc le numérateur et le
dénominateur de a tendent vers 0 , mais à la limite, quand M et P sont
confondus, la droite (MP) devient tangente à la courbe (localement elle la
touche en un seul point) et cette tangente a un coefficient directeur A
qui doit vérifier
A = ![]()
![]()
En effet, qu’on choisisse P à
droite de M ou à gauche de M , dans la situation du
dessin et dans le cas général, la droite (MP) tend vers la même tangente avec
le même coefficient directeur.
|
Si A = on dit que A est le nombre dérivé de f au point x0 ce
qu’on note : A = f’ (x0)
. Dans ce cas, il
existe une tangente unique à la courbe au point M (x0
, f(x0) ) et A est son coefficient directeur. |
De cette définition nous
tirons les conséquences suivantes : f n’admet pas de nombre dérivé en l’un
des ses points si, en ce point la limite
du taux de variation n’existe pas, c'est-à-dire, par exemple :
● Si la
limite est infinie (tangente parallèle à l’axe des y )
● Si la
limite à droite n’est pas égale à la limite à gauche (courbes dont le rayon de
courbure admet une discontinuité, courbes présentant un point dit
« anguleux») .
● Si le
taux de variation oscille sans tendre vers une limite (courbe de sin ![]() au voisinage de 0)
au voisinage de 0)
3 Si f’(x0) existe : dans le voisinage immédiat de M (x0 , f(x0) ), (c'est-à-dire
quand x est dans le voisinage immédiat de x0, très proche de x0,)
courbe et tangente sont pratiquement confondues, ce qui veut dire qu’on peut
faire un amalgame entre l’équation de f(x) et l’équation de la tangente, qui
est généralement moins compliquée. On dit qu’on procède à une approximation affine.
Dans cette région du plan, on
peut écrire que A = ![]() +ε (ε étant
un nombre réel positif ou négatif, très petit et d’autant plus petit que
+ε (ε étant
un nombre réel positif ou négatif, très petit et d’autant plus petit que
x0 – x est petit).
On en déduit que f(x) = f(x0) + A (x – x0) +
ε(x-x0) ou f(x) = f(x0)
+ f’(x0) (x – x0) + ε(x-x0)
Pour traduire que le dernier
terme est négligeable devant les autres, on l’écrit ε(x-x0) =
o(x-x0)
o fonction de (x – x0)
très petite . Ce qui donne finalement
f(x) = f(x0) + f’(x0) (x – x0)
+ o(x-x0) Développement limité
de f(x) au voisinage de x0.
Remarquons qu’au terme o(x-x0)
prés, c’est l’équation d’une droite de coefficient directeur f’(x0).
D’où le terme d’
« approximation affine ». o(x-x0) est l’erreur commise dans l’approximation.
Fonctions dérivables,
fonction dérivée
On
dit qu’une fonction est dérivable sur un intervalle ] a , b[ si elle admet un nombre dérivé en tout
point de ] a,b [ . (On prend un intervalle ouvert pour éviter les problèmes en
a et b) .
La
même définition peut s’appliquer sur Df , le domaine de définition de la fonction. Quand f est
dérivable sur Df, on dit simplement que f est
dérivable.
● Si une
fonction est non définie ou non continue en x0 , il est exclu de
parler de dérivabilité en ce point. Par contre, la notion de dérivabilité
retrouve un sens quand f est prolongée en continuité en x0.
On
démontre que :
Toute fonction dérivable en x0 est continue en x0
Attention : la réciproque n’est pas vraie : il est possible (mais ce n’est pas un
cas courant) de construire des fonctions continues qui n’admettent pas de
dérivée, la fonction étant très « instable » en tous lieux et à
toutes les échelles. C’est le cas notamment des fonctions dont le graphe est
appelé « fractale ».
● Nous
avons vu d’autres cas de non dérivabilité repérés par l’étude de la limite
du taux de variation de f quand x → x0:
points anguleux : limite à gauche ≠ limite à droite
(pour x→|x| en
x = 0 ),
limite infinie (pour x →![]() en x = 0 ) ,
en x = 0 ) ,
limite non existante car f très instable . (pour x → sin ![]() prolongée en
continuité en 0)
prolongée en
continuité en 0)
Dans
le domaine de dérivabilité d’une fonction, on peut définir la fonction x → f ’(x) comme la fonction dérivée de f.
Quelquefois,
l’expression de f’(x) nous permet de repérer des limites infinies et donc de
restreindre le domaine de dérivabilité par rapport à Df , bien que le procédé ne
soit pas trop orthodoxe.
Autres notations de la
fonction dérivée :
● En appelant
(f(x0) –f(x)) : ∆f et (x0 – x) : ∆x
on a f’(x0) = ![]() .
.
Quand
∆x devient très petit, on peut considérer qu’il
prend une valeur idéalement petite dx appelée
différentielle de x (indépendante de x) et il lui correspond une différentielle
de f (contraction de ∆f ) qu’on nomme df (fonction de x)
.
De ce
point de vue, on peut considérer que f’(x) = ![]() . C’est la notation différentielle de Leibnitz.
. C’est la notation différentielle de Leibnitz.
● Quand
f est une fonction de plusieurs variables, par exemple f(x,y,z) dans un domaine
où (par exemple) y et z restent constants f(x,y,z) est une fonction
de x dont on peut calculer la dérivée, qu’on note ![]() .
.
C’est
ce qu’on appelle une dérivée partielle, parce qu’il existe une conception plus
large de la dérivée de f(x,y,z), quand aucune des 3 variables x, y , z n’est
constante.
Règles de calcul des
fonctions dérivées
On
connaît les dérivées des fonctions usuelles x , xn , 1/x , sin x , cos x , ln x , ex
, ….
On
connaît le mécanisme qui permet de calculer à partir des dérivées de f et de g
les
dérivées de λf
, f + λ
, f + g , fg , f / g
les
dérivées de f ○ g ou de f –1
À
partir de là, il y a très peu de fonctions courantes dont on ne sache pas
calculer la dérivée.
Mais
peut être est – il nécessaire de faire une petite piqûre de rappel ?
Dérivées des fonctions
usuelles
|
X n (n ÎN) |
nXn–1 |
Log a x |
1 /
(x ln a) |
Cotan x |
–1–cotan2x |
|
Xa (a ÎR) |
aXa–1 |
Cos x |
–
sin x |
Cotan x |
– 1
/ sin2 x |
|
eλx |
λeλx |
Sin x |
Cos
x |
Arc cos x |
-1 / |
|
ax (aÎR+*) |
ax ln a |
Tan x |
1 +
tan2 x |
Arc sin x |
1
/ |
|
ln |x| |
1/x
|
Tan x |
1 /
cos2 x |
Arc tan x |
1/ (1+x2 )
|
Cosinus, sinus, tangente
hyperboliques
Définitions :
À
rapprocher de la définition de cos, sin, tan à partir des nombres complexes R eiθ
● Ch x =
![]() ● Sh x =
● Sh x = ![]() ● Th x =
● Th x =![]()
À
rapprocher des formules clés de la trigonométrie :
● ch2
x – sh2 x = 1 ● sh(a+b)=sh a ch b + ch a sh
b ● ch (a + b) =ch a ch b + sha shb
Fonctions
réciproques :
● Arg sh x = ln (x + ![]() ) ● Arg ch x = ln (x +
) ● Arg ch x = ln (x + ![]() ) ● Arg th x =
) ● Arg th x = ![]()
Dérivées :
|
Ch x |
Sh
x |
Arg ch x |
1 / |
|
Sh
x |
Ch x |
Arg sh x |
1
/ |
|
Th
x |
1 /
ch2x 1 –
th2x |
Arg th x |
1 /
( 1 – x2) |
|
Coth x |
– 1
/ sh2 x 1 –
coth2 x |
|
|
Opérations sur les fonctions
et dérivées correspondantes :
● Constante K’
= 0 ( K constante)
●
Somme (f + g) ‘ = f’ + g’
● Produit (fg )’ = f’g + g’f si K est
une constante (K f)’ = K f’
●
Quotient ![]()
●(xn)’ = nxn-1 ˜ (![]() )’ = (x ½ )’
= (1/2) x – ½ ˜
(1/x)’ = (x–1)’ = -1 x –2 = -1 / x2
)’ = (x ½ )’
= (1/2) x – ½ ˜
(1/x)’ = (x–1)’ = -1 x –2 = -1 / x2
Fonctions composées
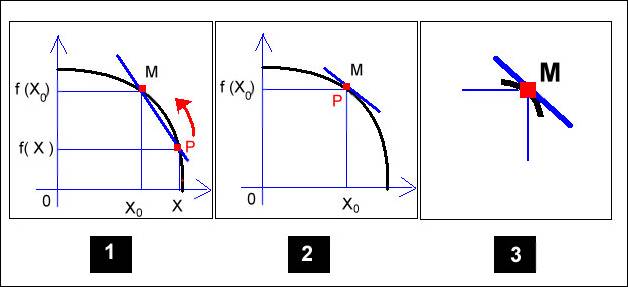
 Dans un double repère
(très inhabituel) on a représenté :
Dans un double repère
(très inhabituel) on a représenté :
●Dans
le 4e quadrant la fonction g
définie sur R+ : x → g (x) =1+![]()
L’image de R+ par cette fonction est [1 ; +∞)
● Dans le 1e quadrant la fonction h : g → h(g) = ln g . C’est la restriction à
[1 ; +∞) de x → ln x . Ce qui signifie que leurs graphes coïncident sur [1 ; +∞).
● Si on veut connaître la valeur de f(x) = ln (1+![]() ) , il faut partir de la valeur de x sur l’axe des x et
suivre le trajet qui est tracé en bleu puis en rouge sur le dessin
) , il faut partir de la valeur de x sur l’axe des x et
suivre le trajet qui est tracé en bleu puis en rouge sur le dessin
1 → (1,2) sur le graphe de g
→ 2 sur l’axe des g
→ (2 , ln 2) sur le graphe de h
→ ln 2
sur l’axe des y . f(1) = ln 2.
En fait, ce processus
correspond à la composition des 2 fonctions
f = h ○
g ou f(x) = h(g(x))
● Si on construisait directement le graphe de y
= f (x) = ln (1+![]() ) , il serait évidemment différent du graphe de
ln (g) car l’axe des abscisses serait « gradué en x » alors que dans notre dessin, il est
« gradué en g » qui est déjà le résultat de l’application d’une
fonction à la variable x
) , il serait évidemment différent du graphe de
ln (g) car l’axe des abscisses serait « gradué en x » alors que dans notre dessin, il est
« gradué en g » qui est déjà le résultat de l’application d’une
fonction à la variable x
Si j’écris f(x) = ln (1+![]() ) f peut être indifféremment considérée comme une fonction de
x ou comme une fonction de g si on pose g(x) : x → 1+
) f peut être indifféremment considérée comme une fonction de
x ou comme une fonction de g si on pose g(x) : x → 1+![]() et h(x) : x → ln x on peut écrire f(x) = h (g(x)) = h ○ g (x) = ln (g(x)) .
et h(x) : x → ln x on peut écrire f(x) = h (g(x)) = h ○ g (x) = ln (g(x)) .
Ecrire f(x) = ln
(g(x)) revient à considérer f comme une fonction de g. Mais attention
, cette fonction n’est pas f(g(x)) car en toute logique f(g(x)) devrait
être la fonction x →ln (1+![]() ). On peut par contre écrire f (x)= h(g(x))
.
). On peut par contre écrire f (x)= h(g(x))
.
Si on considère f
comme une fonction de x , f(x) = ln (1+![]() ) admet pour dérivée f’(x) , la dérivée cherchée .
) admet pour dérivée f’(x) , la dérivée cherchée .
Si on considère f comme une fonction de g, f(g) = ln (g) , c’est qu’on a procédé au changement de
variable g = 1+![]() et dans le nouveau repère, f (g) admet aussi une dérivée par
rapport à g : f’(g) =
et dans le nouveau repère, f (g) admet aussi une dérivée par
rapport à g : f’(g) = ![]()
Pour distinguer ces 2 dérivées on peut les appeler f’(x) ou f’(g) qu’on lira respectivement dérivée de f par rapport à x et dérivée de f par rapport à g , cette dernière écriture supposant que dans f on considère g comme une variable, alors qu’il s’agit en réalité d’une fonction de x.
On a donc fait un changement de variable x → g = 1+![]()
Dans la figure qui illustre ce paragraphe, si on écrit f : x
→f(x)=ln (1+![]() ) puis f (g) = ln (g) en posant g =1+
) puis f (g) = ln (g) en posant g =1+![]() ,
,
● la dérivée de la fonction bleue
x → g (x) = 1+![]() est g’ (x)
c'est-à-dire
est g’ (x)
c'est-à-dire ![]()
● et la dérivée de la fonction rouge f(g) : g → ln g est f’(g) c'est-à-dire ![]()
On va
démontrer que si dans f(x) on fait le changement de variable g = g(x) alors f’(x)
= f’(g) . g’(x)
On a ![]() d’où on déduit par
passage aux limites que f ’ (x) = f ’ (g) . g’ (x)
d’où on déduit par
passage aux limites que f ’ (x) = f ’ (g) . g’ (x)
Et si
on fait le changement de variable inverse dans f’(g) :
g →
x : f’ (x) = f ’ (g (x)) . g’ (x)
Et
comme la composition de deux fonctions peut être assimilée à un changement de
variable :
Si
f = h ○ g : f’ (x) = h ’ (g)
. g’ (x) avec h’(g) = f’(g) dans le précédent changement de variable (puisque h(g) = ln (g) et f(g) = ln (g)
dans notre exemple) et donc f’(x) = h’(g(x)). g’(x)
● Par exemple on cherche la dérivée de (2X2 + 3)5
. on pose g = (2X2 + 3) et on a f = g 5
.
On
dérive f par rapport à g on trouve 5 g 4 .
On dérive g par rapport à X on trouve 4X .
On
multiplie les 2 dérivées : 4X (5 g4 )
= 20X (2X2+3)4 . C’est la dérivée cherchée.
● Autre exemple : on cherche la dérivée de ln f(x)
sachant que la dérivée de ln (x) est 1/x
Avec
la loi de dérivation des fonctions composées on trouve (ln f
) ‘ = ![]() (à retenir)
(à retenir)
● de la
même façon (e f
) ‘ = f’ e f ● (sin (x2))’ = 2X
sin (x2) ● si x > 0 : (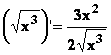
Dérivée de la fonction
réciproque :
Supposons
f bijective sur Df à valeurs dans f(Df) . f est dérivable sur Df et
sa dérivée est f’(x).
f
admet une fonction réciproque, elle aussi dérivable sur f(Df) qu’on note f – 1 (x) et qui admet pour
dérivée (f – 1 ) ‘ (x) .
Par
définition de la fonction réciproque, si y = f(x) on a x = f – 1 (y) et donc x = f – 1 (f(x)) qui est une fonction composée
I = f -1 ○ f . On a donc x en fonction de y et y en
fonction de x
Si on dérive x = f(y) par rapport à x on trouve x’(x) = 1 = x’(y) . y’(x) (fonction composée)
Il faut lire x’ (y) comme « la dérivée que nous cherchons, dérivée de
f – 1 ,
par rapport à y » .
On
connaît y’(x) qui est
la dérivée f’(x) . On s’arrange pour exprimer y’(x) en fonction de y :
et on
obtient x’(y) en
fonction de y qui est la dérivée cherchée , mais en
fonction de y au lieu de x.
Exemple 1 : On cherche la dérivée de arc cos
(x). Prenons y = f(x)
= cos x
●(E) : x = arc cos y
● dérivons (E) par rapport à x : 1 = arc cos’(y) . y ‘ (x) donc
1 = arc cos ’ (y)
. ( - sin x)
● remplaçons –
sin x par sa valeur en fonction de y = cos x
on obtient – sin x = – ![]()
1 = arc cos’(y) (-1![]() ) on en déduit que arc cos’(y) =
) on en déduit que arc cos’(y) =  (expression finale)
(expression finale)
Ou,
ce qui revient au même : (arc cos) ‘ (x)
= ![]() qui est la dérivée
cherchée.
qui est la dérivée
cherchée.
Exemple 2 : On cherche la dérivée de ex sachant que si y = ln x on a
(E) : x =
ey .
Dérivons
(E) par rapport à x : 1 = (ey)
’ (y) . y’(x) =
(ey) ’
(y) .
![]() et comme x = ey : 1 = (ey)’ (y) .
et comme x = ey : 1 = (ey)’ (y) . ![]()
D’où
on tire ( ey )’ (y) = ey (la dérivée de e y
par rapport à y est ey )
La
dérivée de e x par rapport à x est donc e x .
Le
processus de calcul est moins compliqué que la formule ![]() ne le laisse supposer.
ne le laisse supposer.
Dérivées d’ordre supérieur
● la
dérivée de f si elle existe est notée f’ ou f(1) . On dit qu’elle
est d’ordre 1
● la
dérivée de f’ si elle existe est notée f’’ ou f(2) . On dit qu’elle
est d’ordre 2
Et
ainsi de suite …
Si la
dérivée d’ordre k existe et qu’elle est dérivable on note f (k+1) =
(f (k) )
‘
Par
extension on dit que f = f 0 .
En
notation différentielle on considère que ![]() est un opérateur de
dérivation par rapport à x .
est un opérateur de
dérivation par rapport à x .
On
devrait donc noter la dérivée seconde 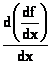 mais par soucis de
simplification on l’écrit
mais par soucis de
simplification on l’écrit ![]()
Exemple
si f : x → xp alors avec n < p f(n) = p (p-1) (p – 2) …(p – n +
1) x p – n
Notion de classe
On
dit que f ∈ Cn (classe n ) si f est
n fois dérivable sur E et que f(n) est continue sur E .
Si f ∈ C0 elle est continue et pas nécessairement dérivable.
Si f ∈ Dn elle est n fois dérivables
mais f (n) n’est pas forcément continue
Rappelons
que f dérivable impliquant f continue, les dérivées
d’ordre inférieur à l’ordre de la classe sont forcément continues.
C∞ est la classe des fonction
pour lesquelles Cn existe quel que soit n
C’est
le cas de beaucoup de fonction usuelles (les polynômes finissent par donner une
constante non nulle puis 0, mais f = 0 est une fonction dérivable de dérivée 0)
● f bijective : Si f ∈ Cn et f ’(0) ≠ 0 alors f-1 ∈ Cn
Formule de Leibnitz
(fg) (n)
= 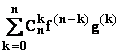 à rapprocher du
binôme de Newton (a+b)n =
à rapprocher du
binôme de Newton (a+b)n = 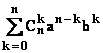
Rappelons
que ![]() avec Cn0
= 1 par convention
avec Cn0
= 1 par convention
et
que pour n entier naturel, n ! = n
(n–1)(n-2) …..(2)(1) avec 0 ! = 1 par convention
|
N ↓ P→ |
0 |
1 |
2 |
3 |
4 |
|
1 |
1 |
1 |
|
|
|
|
2 |
1 |
2 |
1 |
|
|
|
3 |
1 |
3 |
3 |
1 |
|
|
4 |
1 |
4 |
6 |
4 |
1 |
Le
triangle de Pascal pour obtenir facilement Cnp
en fonction de n et p.
On
écrit 1 , 1 sur la première ligne . Puis, chaque ligne
contient une case de plus que la précédente, commence par 1 et finit par 1 ,
les cases intermédiaires sont obtenues par addition de 2 cases de la ligne
supérieure (celle qui est immédiatement au dessus de la case à remplir et celle
qui est à sa gauche). On peut poursuivre
pour n et p = 5, 6, etc ..
Exemple
(fg)(3) = 1.f(3).g + 3.f(2).g(1)
+ 3.f(1).g(2)
+ 1.f.g(3)
. (ligne N = 3 du tableau)
Propriétés des fonctions
dérivables
Lemme de Rolle
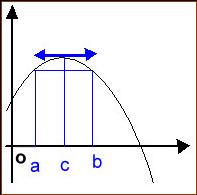 f continue sur [ a ;
b ] et dérivable sur ] a ; b [ telle que f(a) = f(b)
f continue sur [ a ;
b ] et dérivable sur ] a ; b [ telle que f(a) = f(b)
Alors,
il existe un nombre c sur ] a ; b [ tel que f’(c)
= 0
Autrement
dit , il y a un point sur ] a ; b [ où la
tangente à la courbe est parallèle à l’axe des x .
Si f
est constante, le résultat est trivial, si elle n’est pas constante, elle admet
un maximum ou un minimum sur l’intervalle. Donc une tangente // Ox .
Accroissements finis
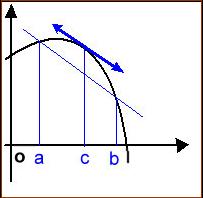 f continue sur [ a ;
b ] et dérivable sur ] a ; b [
f continue sur [ a ;
b ] et dérivable sur ] a ; b [
Il
existe sur ] a ; b [ une tangente parallèle au
segment de droite qui joint les points (a ; f(a) et (b ; f(b) ) .
Autrement dit, il existe entre a et b un nombre c tels que
f’(c)
= ![]() (coefficients
directeurs des 2 droites parallèles)
(coefficients
directeurs des 2 droites parallèles)
Conséquence sur les variations
de f
Supposons
la dérivée de f positive sur ] a ; b [ .
Quels
que soient x1 et x2 ∈ ] a ; b [ , il existe un nombre c ∈ ] x1 ; x2[
tel que ![]() = f’(c)
= f’(c)
et
comme f’(c) est positif par hypothèse ,
f(x1)
– f(x2) est du même signe que x1 – x2 ce qui
est la définition même d’une fonction croissante.
Continuité de la dérivée f ‘
f
continue sur [ a ; b ] et dérivable sur ]
a ; b [ . f ’ est – elle continue ?
Soit
x0 ∈ ] a ; b [ , f’ est
continue en x0 si lim f’(x) quand x → x0 existe et est
égale à f’(x0)
Appelons
T (x0 , x) le taux de variation de
f : [f(x0) – f(x) ]
/ [ x0 – x ]
du
moment que f est dérivable, il a une limite quand x → x0 et cette limite
est f’(x0).
À
tout x correspond une valeur c(x) comprise entre x0 et x telle que f’(c(x)) = T (x0 ,
x)
Mais
quand T (x0 , x) est très proche de
f’(x0) ce n’est pas parce qu’il existe un point c entre x0
et x
tel que f’(c) soit aussi proche de f’(x0) que T(x0 ,
x) que c’est le cas de tous les points entre x0 et x.
La
fonction f peut être relativement stable et la fonction f’ très instable. Donc,
il n’est pas sûr que
![]() existe et soit la
limite des f’(c(x)) définis comme précédemment .
existe et soit la
limite des f’(c(x)) définis comme précédemment .
Donc : il n’est pas sur
que la fonction dérivée soit continue.
Ceci
dit, si ![]() existe, les deux
limites sont bien sûr égales.
existe, les deux
limites sont bien sûr égales.
On
peut avoir la même discussion quand on prend x0 = a (ou b) .
Si ![]() existe et est finie
alors f est dérivable à droite et
existe et est finie
alors f est dérivable à droite et ![]() =f’(a)
=f’(a)
Si ![]() =±∞ f n’est pas
dérivable en a et f’(a) n’existe pas (exemple de 1 / x
en 0 )
=±∞ f n’est pas
dérivable en a et f’(a) n’existe pas (exemple de 1 / x
en 0 )
● Mais il
existe des fonctions partout dérivables comme x2 sin (1 / x2)
prolongée en continuité en 0 dont la fonction dérivée n’admet pas de limite
quand x → a
(ici a = 0)
|
1) on fait le changement de variable u = 1/x
et on obtient f(u) = (sin u2) / u2
. Quand x → 0 ,
u → ¥ et donc à la limite f(u) → 0 . On peut
donc écrire f(0) = 0 2) f est dérivable en 0 si ce qui par le même changement de variable que
précédemment donne (sin u2) / u qui tend vers 0 quand u →∞. On peut donc écrire que f’(0)
= 0 . Donc f est partout dérivable. 3) La dérivée de f est f’(x) = 2x sin (1/x2)
– cos(1/x2) / x et on a vu que quand x →0 , le 1er terme
tend vers 0 . Mais pour le second, quel que soit ⍺ très voisin de 0 on peut le
rendre aussi grand que l’on veut dans l’intervalle E =[
0 , ⍺] , puisque dans E , il
existe une infinité de valeurs de x aussi petites que l’on veut pour lesquelles
le cosinus est égal à 1 et donc le second terme égal à 1/x . Donc,
f’ ne peut avoir en 0 une limite finie et f continue et partout dérivable ne signifie
pas que f’ est continue. |
Calcul de certaines limites
Des
expressions telles que f(x) = ![]() ou g(x) =
ou g(x) = ![]() peuvent être
transformées en :
peuvent être
transformées en :
f(x)
= ![]() ou g(x) =
ou g(x) = ![]() et on reconnaît un T(0,x) dont la limite quand x → 0 donne un nombre dérivé
et on reconnaît un T(0,x) dont la limite quand x → 0 donne un nombre dérivé
![]() f(x) = (ex)’(0) = e0
= 1 ou
f(x) = (ex)’(0) = e0
= 1 ou ![]() g(x) = (sin x)’(0) = cos (0) = 1
g(x) = (sin x)’(0) = cos (0) = 1
C’est
donc un moyen de calculer ces limites à bon compte, en les amalgamant à des
nombres dérivés.
L’inégalité des accroissements
finis
Si f
est dérivable sur ]
a ; b [ et que f’ est continue sur cet intervalle .
De f’
continue on tire f’ bornée sur ] a ; b [ et donc m ≤ f’ ≤ M
(m et
M sont déduits de l’étude des variations de f’(x) sur ]
a ; b [ )
Du
théorème des accroissements finis, on déduit : m ≤ ![]() ≤M
≤M
Et finalement,
comme b – a est positif : m (b – a ) ≤ f(b) – f(a) ≤ M (b – a)
● Dans le même
ordre d’idée :
f lipschitzienne si |
f(x) – f(y)| ≤ K | x –y| (contractante
si K < 1)
● Exemples d’utilité : on connaît m , M et f(0) = 0 on peut écrire m x ≤ f(x) ≤ M x
(ln
x)’ = 1/x et pour x∈ [1 , +∞) 0 < 1/x ≤ 1 et ln (1) = 0
d’où 0 (x–1) ≤ ln x ≤ 1(x –1) ou ln x ≤
x
Formules d’ordre 1 de Mac Laurin et de Taylor
Si f
est une fonction de classe C1 (dérivable ,
dérivée continue)
De
f’(c) = ![]() on déduit qu’il existe
un nombre θ tel que 0< θ
< 1 et c = θ x ce qui donne
on déduit qu’il existe
un nombre θ tel que 0< θ
< 1 et c = θ x ce qui donne
Pour
tout x ∈ [ 0 ; x] : f(x) = f(0) + x f’(θ
x) Mac Laurin
Pour
tout x ∈ [ a ; x] :
f(x) = f(a) + (x–a) f’ (a + θ (x–a)) Taylor
À
rapprocher du développement limité d’ordre 1 au voisinage immédiat de a :
f(x) = f(a) + (x–a)f’(a) + o(x-a) si θ (x–a) est négligeable
Formules générales de Mac Laurin et de Taylor
Si f ∈ Cn et que f(n) est dérivable . Avec 0 < θ < 1 on a
Ne peut être négligé à priori
![]()
f(a+h) = f(a) + hf(1)(a) +
![]() f(2)(a)+…+
f(2)(a)+…+ ![]() f(n)(a) +
f(n)(a) + ![]() f(n+1)(a+θh) Taylor
f(n+1)(a+θh) Taylor
f(h) = f(0)
+ hf(1)(0)
+ ![]() f(2)(0)+…+
f(2)(0)+…+ ![]() f(n)(0) +
f(n)(0) + ![]() f(n+1)(θh) Mac Laurin (a = 0)
f(n+1)(θh) Mac Laurin (a = 0)
Utilisation géométrique de la
dérivée seconde
Fonctions
de la classe C2
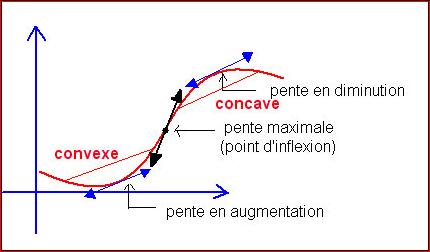 f ’’ >0 équivaut à f ’ croissante (la pente de la
tangente augmente)
f ’’ >0 équivaut à f ’ croissante (la pente de la
tangente augmente)
f concave : graphe en dessus des
sécantes f ’’ < 0 pente diminue
f convexe : graphe en dessous des
sécantes f ’’ > 0 pente augmente
Point d’inflexion : f ’’ =
0 (tg pas forcément horizontale)
Si f
convexe : f ’ augmente entre x et y alors f ’ est majorée par f ’(y)
On en
déduit (accroissements finis) que si X et Y appartiennent à une portion convexe
et C entre X et Y :
f ’(c)= 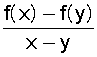 ≤ f ’ (y)
≤ f ’ (y)
Plus
précisément, sur
une partie convexe du graphe, toute sécante AB (B à droite de A) a un
coefficient directeur inférieur ou égal à celui de la tangente en B.
Remarquons
que dans la langue courante on dirait plutôt au sujet d’un relief qu’un trou est
concave et une montagne convexe (est concave ce qui est creux et convexe ce qui
est bombé) .
En
mathématiques, si on assimile (abusivement) l’axe des x au niveau horizontal,
c’est plutôt le contraire : ce qui tend à dominer l’horizontale est
concave et ce qui tend à passer sous l’horizontale est convexe.
Mais
bon, ne prenez pas cette remarque au pied de la lettre et examinez plutôt la
position relative des sécantes et de la courbe.
Remarquons
aussi que la fonction dérivée peut très bien être décroissante avant le point
d’inflexion et croissante après.