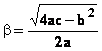Equations différentielles

Définition : Une équation différentielle d’ordre n est une équation qui associe

● une fonction inconnue y= f(x), et certaines de ses dérivées jusqu’à l’ordre n (y, y’, y’’, …y⁽ⁿ⁾ ),

● des fonctions arbitraires de x (ou des constantes) connues .

C’est l’ordre maximum de la dérivée de y dans l’équation différentielle qui détermine son ordre.

Equations différentielles du premier ordre :

Type 1.1 : équations à variables séparables

Si après avoir écrit y’ = dy / dx on parvient à une équation de type f(x)dx = g(y).dy, les variables étant nettement séparées, il suffit d’intégrer les deux membres, en faisant apparaître la constante d’intégration (C) et on obtient une nouvelle équation de type F(x) = G(y) + C qui dans certains cas permet d’exprimer y en fonction de x . La famille de fonctions y ainsi obtenue peut ensuite être soumise au filtre des « conditions initiales » pour préciser la fonction recherchée.

Exemple 1 :

x + yy’ = 0 d’où, on tire xdx = - ydy (les variables sont bien séparées) .

On intègre les deux membres : d’où x² + y² = 2C

Si 2C est positif, on le pose égal à R² et on retrouve l’équation d’un cercle centré en O de rayon R.

R peut être déterminé grâce aux conditions initiales.

Exemple 2 :

y’– d’où on tire (variables séparées)

On intègre et on obtient –ln (1–y) = ln(1+x) +C et en posant C = ln k →

y = où a peut être déterminé grâce aux conditions initiales.

Type 1.2 : Equations homogènes.

C’est une équation différentielle qu’on peut mettre sous la forme y’ = f(y/x) , y et x ne se retrouvant dans l’équation qu’au sein d’une fraction de ce type.

Si on pose t = notre équation devient y’ = f(t) et on a par ailleurs dy = xdt + t dx

On en tire . On a donc = y’ = f(t) = x

Et on peut à ce stade séparer les variables : ce qui nous renvoie au Type 1.

Exemple 1

(x²+y²)dx–xydy=0 qui donne en divisant tout par y² → 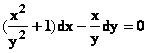→ 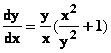Type 2

En posant t = → = f(t) = → f(t) – t = → Type 1

En intégrant : ln kx = (la constante d’intégration est dans le logarithme) → on en déduit y.

Exemple 2

xdy –ydx = → 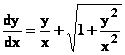et ainsi de suite … jusqu’à Type 1

Type 1.3 : Equations linéaires sans second membre.

Une équation différentielle du 1^er ordre est dite linéaire si elle est de la forme y’ + y.a(x) = b(x)

Elle est dite sans second membre si b(x) = 0 . Soit y’ + y.a(x) = 0 .

À partir de là, on obtient Type 1 (variables séparées) et on peut opérer.

On obtient une solution de type y = K e^–A(x) avec A primitive de a

Remarque : y’ f(x) + y g(x) = 0 se ramène au cas précédent en divisant l’équation par f(x) .

Exemple 1 :

y’+2xy = 0 → → en posant C = ln k on obtient → y = k

Type 1.4 : Equations linéaires avec second membre

y’ + y.a(x) = b(x)

On utilise la méthode de variation des constantes (Lagrange)

1) On résout l’équation sans second membre y’ + y.a(x) = 0 et on trouve y = K e^–A(x)

2) on dit que y est solution de l’équation avec second membre à condition que K soit considérée non pas comme une constante mais comme une fonction de x.

3) On dérive y (avec K fonction de x ) on trouve → y’ = K’(e^–A(x)) – Ka(x) e^–A(x)

4) On reporte cette valeur de y’ dans l’équation initiale, ce qui nous permet de calculer K’ puis K

K’(e^–A(x)) – Ka(x) e^–A(x) + (K e^–A(x)) a(x) = b(x) → K’(e^–A(x)) = b(x) → K’ = b(x)( e^A(x)) Type 1 → K

5) En remplaçant K par sa valeur dans y = K e^–A(x), on a la solution cherchée.

Remarque : y’ f(x) + y g(x) = h(x) se ramène au cas précédent en divisant l’équation par f(x)

Exemple 1 :

y’cos x + y sin x = 1

1) sans second membre : → ln y/k = ln cos x → y = k cos x (Ke^-A(x)= K e^{(ln cos x)} )

3) on dérive y avec k fonction de x y’ = k’ cos x – k sin x

4) on reporte les valeurs de y et y’ dans l’équation initiale : k’cos² x – k cos x sin x + k sin x cos x = 1

On en déduit que k’ cos² x = 1 → k’ = 1 / cos² x → k = tan x + C

5) On reporte la valeur de k dans y = k cos x → y = sin x + C cos x (solution cherchée)

Exemple 2 :

y’ – y/x = x²

1) sans second membre dy / y = dx / x → y = k x

3) dérivons avec k fonction de x → y ‘ = k’x + k

4) reportons y et y’ dans l’équation initiale k’x + k –k = x² → k’ = x → k = x² / 2 + C

5) remplaçons k par sa valeur dans y = kx → y = x³ / 2 + Cx

Type 1.5 : Cas particulier → coefficients et second membre constants

y’ + ay = b ( avec a et b constantes)

On sépare facilement les variables et on résout .

Type 1 → x = → b – ay = k e^–ax → y = e^–ax

Exemple 1 :

y’ – 4y = 2

d’où et enfin → y = Ce^4x

Equations différentielles du second ordre incomplètes

Type 2.1 : la fonction n’apparaît que par ses dérivées y’’ et y’ .

On se trouve confronté à la forme générale y’’ = f(x,y’) et en posant y’ = z notre équation devient

z’ = f(x,z) ce qui nous ramène au premier ordre.

On peut donc déterminer z et y est l’une de ses primitives.

Exemple 1 :

2y ’’ = on pose z = y’ et l’équation devient 2z’ = (1^er ordre) →

on en déduit arg sh z = et donc z = sh = y’

on intègre y’ pour trouver y – y₀ = 2 ch (x₀ et y₀ sont liés aux constantes d’intégration)

Type 2.2 : seule la dérivée seconde apparaît

La forme générale est donc y’’ = a(x). Il suffit d’intégrer deux fois a(x) pour trouver y

Exemple 1 : chute des corps (y est une fonction du temps t )

L’accélération du mouvement est constante : y’’ = g (équation initiale)

Première intégration y ‘ = gt + V₀ (y’ est la vitesse au temps t et V₀ la vitesse au temps t = 0 )

Deuxième intégration : y = gt² + V₀t + y₀ (y₀ est l’abscisse du corps en chute au temps t = 0)

Type 2.3 : La variable x n’apparaît pas explicitement

La forme générale est f(y, y’, y’’) = 0.

1) on pose p = y’ et on considère p comme une fonction de y

On a y’’ = , l’équation initiale devient f(y, p, ) ce qui nous ramène au 1^er ordre ,

p étant la fonction et y la variable. On peut donc trouver p en fonction de y

2) dans l’équation initiale on a donc y’ en fonction de y et y ‘’ étant évaluée comme on peut dire qu’il s’agit du produit d’une fonction de y (dp / dy) par y’ (dy / dx).

En somme notre équation initiale devient f(y , y’) = 0 et on retombe sur le 1^er ordre.

3) Assez communément y ’ n’intervient que par son carré y ’². Dans ce cas, on a intérêt à poser

q = y’² ce qui donne soit y’’= avant de procéder comme précédemment .

4) Quand l’équation est de la forme y ‘’ + a y ‘ + b y = 0 , (a et b constantes) il existe une technique de résolution plus simple qui sera exposée plus loin.

Exemple 1 :

y’’ = e^2y avec y(0) = y ’(0) = 0

Posons y ’ ² = q , on a y’’= . Notre équation devient = e^2y soit dq = 2e^2y dy

Et donc on a q en fonction de y → q = e^2y + K (K = –1 d’après les conditions initiales)

y’ = ± (ordre 1 )

On sépare les variables, dx= ± ±

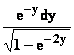
on fait le changement de variable t = e^-y et on trouve finalement y = – ln cos x.

On trouverait le même résultat à partir de p = y ’

Equations différentielles linéaires du second ordre

Type 2.4 : à coefficients constants, mais sans second membre .

ay’’ + b y’ + cy = 0.

● Si a = 0 et b ≠ 0 nous retrouvons le 1^er ordre. La solution est y =ke^rx avec r = –c / b

● Si a ≠ 0 nous allons chercher une solution de type y = Ke^rx avec r complexe.

Nous avons y = Ke^rx , y’ = r Ke^rx et y’’ = r² Ke^rx donc l’équation devient Ke^rx (ar² +br +c) = 0

D’où nous déduisons que ar² +br +c = 0 → r racine du polynôme caractéristique aX² + bX + c

Si le polynôme admet deux racines distinctes réelles r₁ et r₂

Les solutions sont de la forme y = k₁e^r1x + k₂e^r2x (où k₁ et k₂ sont des nombres complexes)

Si le polynôme admet une racines double réelle r

Les solutions sont de la forme y = e^rx (mx + p) (où m et p sont des nombres complexes)

Si le polynôme admet deux racines complexes conjuguées r₁ et r₂

Les solutions sont de la forme y = k₁e^r1x + k₂e^r2x (où k₁ et k₂ sont des nombres complexes)

Dans ce dernier cas, en posant et si on choisit k₁ et k₂ conjugués et qu’on pose

c₁ = k₁ + k₂ , c₂ = i(k₁ –k₂). Les nombres c₁ et c₂ sont réels et on débouche sur

y=e^ax(c₁cos βx +c₂sin βx) qu’on peut écrire sous la forme y = M e^ax sin (βx – g)

Avec M² = c₁² + c₂² , sin g = c₁ / M et cos g = c₂ / M

Exemple 1 :

2 racines réelles →k₁e^r1x + k₂e^r2x

y’’ – 5y’ +4y = 0

a = 1 b = –5 c =4 → équation caractéristique X² – 5X + 4 → 2 racines r₁ = 1 et r₂ = 4

Solutions de type K₁ e^x + K₂e^4x

Exemple 2 :

racine double → y = e^rx (mx + p)

y’’+2y’ +1

a = 1 , b = 2 , c =1 → équation caractéristique X² +2X + 1 → 1 racines double r = –1

Solutions de type e–^x (mx + p)

Exemple 3 :

2 racines complexes → y = e^ax(c₁cos βx +c₂sin βx)

y’’ +y = 0 (équation du pendule)

a = 1, b = 0 , c = 1 polynôme caractéristique X² + 1 = 0 → solutions complexes r₁ = i et r₂ = – i

a = 0 (Partie réelle des racines) et β = 1 (Partie imaginaire) solutions de type y = c₁ cos x + c₂ sin x

Approche vectorielle (pour les esthètes)

On peut associer toute équation différentielle linéaire à coefficients constants et sans second membre à un système différentiel d’ordre 1.

Et ce système différentiel est associé à une matrice de rang 2 .

Par exemple on associe y’’ + ay’ + by = 0 à un système différentiel d’ordre 1 qui s’écrit

On démontre que l’ensemble des solutions de ce type d’équation est dans chaque cas un espace vectoriel de dimension 2 sur un corps Q .

Il suffit donc de trouver 2 solutions linéairement indépendantes et elles forment une base de cet espace vectoriel. (On peut dissocier les cas où Q = R et Q = C )

Le polynôme caractéristique de la matrice s’écrit X² +aX + b et il admet pour racines les valeurs propres associées à l’application linéaire.

On discute ensuite l’existence et la nature de solutions indépendantes selon l’existence et la nature de valeurs propres :

2 valeurs propres réelles → e^λ1x et e^λ2x ou encore e^axchβx et e^axshβx (λ₁=a+β, λ₂=a-β)

une valeur propre double →e^λx et x e^λx

2 valeurs propres complexes conjuguées →e^axcos βx et e^axsin βx (λ₁=a+iβ, λ₂=a-iβ)

Type 2.5 : Equations linéaires à coefficients constants avec second membre particulier

ay’’ + by’ + cy = f(x) (1)

ay’’ + by’ + cy = 0 (2)

● On obtient les solutions de (1) en ajoutant à z la solution générale de (2) une solution particulière w de (1). En effet, si y = z +w on a y’ = z’ + w’ et y’’ = z’’ + w’’ .

Si w est une solution particulière de (1), on a bien aw’’ + bw’ + cw = f(x) et donc

a( y’’–z’’ ) + b( y’–z’ ) + c( y–z ) = f(x) mais comme az’’ + bz’ + cz = 0 (z étant une solution particulière de (2)) il vient que ay’’ + by’ + cy = f(x) et y est bien une solution de (1) . On démontrerait de la même façon que si y est une solution de (1) et z une solution de (2) , alors w = y – z est une solution de (1).

● on se cantonne au cas où le second membre, f(x) = Q(x) e^mx , Q étant un polynôme et m un nombre complexe . Ce cas englobe les cas suivants :

→ f(x) = constante → f(x) = exponentielle → f(x) = polynôme

→ f(x) = sinus ou cosinus (formule d’Euler) → f(x) = produit d’un sinus (ou cosinus) par polynôme

● Il existe une solution w de type e^mxR(x) où R est un polynôme

w = e^mxR(x) il ressort que w’ = e^mx( mR(x) + R’(x)) et w’’ = e^mx( m²R(x) + 2mR’(x)+ R’’(x))

(1) donne e^mx [ aR’’ + (2am+b)R’ + ( am²+bm+c)R ] = Q(x) e^mx

Posons aX²+bX+c = P(X) → On a 2aX+b = P’(X) qui s’annule pour X = –b/2a et il reste

a R’’ + P’(m)R’ + P(m)R = Q d’où on déduit que

Si m n’est pas racine de P → d°(R) = d°(Q)

Si m est racine simple de P → d°(R) = d°(Q)+1 d°(R)= d°(Q) + multiplicité de m en racine de P

Si m est racine double de P → d°(R) = d°(Q) +2 .

Une fois le degré de R connu, on obtient ses coefficients par identification.

Une fois connue W , on l’ajoute à une solution de l’équation sans second membre

.

En pratique

1) On cherche les solutions de l’équation sans second membre.

On trouve un truc du genre k₁ e^px +k₂e^qx ou e^px (mx + p) ou e^px (k1 cos β x + k2 sin β x)

2) On identifie m sans problème si le second membre est de la forme d’un polynôme Q(x) (m = 0) ou par exemple de la forme e^2x (Qx) : m = 2 . Mais si le second membre est par exemple sin x , on l’écrit

et on considèrera que notre solution particulière sera la somme d’une solution avec second membre égal à e^ix/2i et d’une solution avec second membre égal à – e-^ix/2i (m = i puis –i) .

3) Une fois identifié m, on a le degré du polynôme R qui est au moins égal au degré de Q le polynôme du second membre. On écrit par exemple R = AX² + BX + C et S = e^mx.R(x) la solution particulière recherchée.

4) On cherche S’ et S’’ et on reporte S, S’ et S’’ dans l’équation initiale aS’’ + bS’ + cS = e^mxQ(x)

le premier membre s’écrit e^mxQ(A, B , C, x) . On identifie les coefficients A, B, C de R en égalant le polynôme Q(A, B,C ,x) et le polynôme Q(x).

5) Mais attention : supposons que les solution de l’équation sans second membre soient par exemple

k₁+ k₂e^2x et que la solution particulière recherchée soit de la forme e^2x (Ax² + Bx + C).

N’oublions pas que par la suite, il nous faudra ajouter la solution sans second membre et la solution particulière pour trouver la solution finale. Or, il arrive que la forme générale de la solution sans second membre englobe une partie de la solution particulière et nous devons éviter les redondances.

Par exemple, ici, nous n’avons pas à chercher le coefficient C car C e^2x figure déjà dans k₂e^2x . Posons C = 0 .

De la même façon, si la solution recherché est de la forme Ax² + Bx + C nous n’avons pas à chercher C car C figure déjà dans la solution sans second membre sous la forme k₁ . ( C = 0)

Si la solution sans second membre était du type e^2x (mx + p) et la solution particulière recherchée du type e^2x (Ax² + Bx + C) c’est le calcul de B et C qui serait superflu car e^2xBx figure dans e^2x mx et e^2xC figure déjà ans e^2xp (B = 0 et C = 0) .

6) Enfin ajoutons la solution sans second membre et la solution particulière e^mx.R(x) pour donner la solution générale recherchée.

Type 2.6: Equations linéaires à coefficients non constants sans second membre

Cette fois, les coefficients a, b, c sont des fonctions de x.

a(x)y’’ + b(x)y’ + c(x)y = f(x) (1) avec second membre

a(x)y’’ + b(x)y’ + c(x)y = 0 (2) sans second membre

Comme dans le cas où a, b , c sont des constantes, l’ensemble des solutions de l’équation sans second membre forme un espace vectoriel de dimension 2.

Il nous faut donc trouver 2 solutions linéairement indépendantes pour en avoir une base.

Supposons qu’on connaisse une solution de (2)  : s

Soit z une fonction inconnue de x

Posons y = zs et cherchons sous quelles conditions, y peut être une solution de (2).

En dérivant 2 fois y et en intégrant les valeurs obtenues à (2), on obtient :

(as)z’’ + (2as’ +bs)z’ + (as’’+bs’+cs)z = 0

Le terme en z étant nul puisque s est solution de (2), il reste

(as)z’’ + (2as’ +bs)z’ = 0 (3) où a , b, s et s’ sont des fonctions connues et z le fonction inconnue.

Or, on a vu que par un changement de variable de type w = z’, on se trouvait en présence d’une équation différentielle du 1^er ordre à variables séparables.

Donc si on peut résoudre (3) et trouver la valeur de z (ce qui est généralement possible) ,

y = zs est bien solution de (2 ).

Soit z et zs sont indépendantes, soit zs est formée d’une combinaison linéaire de s et d’une autre fonction qui constitue le 2^e vecteur de la base.

Exemple 1 :

y’’tan(x) + y’(tan² x –2) + 2ycotan x = 0 avec x Î [0, π/2] sachant que s = sin x est solution

On cherche z telle que y = zs soit solution et on trouve z = k₁ sin x + k₂.

y = k₁ sin² x + k₂sinx est donc solution et { sin²x ; sin x } .constitue une base de l’ensemble des solutions.

Résolution à l’aide des séries entières

Supposons que s soit développable sous la forme

S = a₀ + a₁ x + …+a _n xⁿ + …

Alors, on peut dériver s pour obtenir les séries s’ et s’’

S’ = a₁ + 2a₂x + …. + na_nx^n-1+ …

S’’ = 2a₂ + ……+ n(n–1)a_nx^n–2 +…

Dans les cas fréquents où les coefficients de l’équation différentielle sans second membre sont des polynômes, on va trouver en reportant chaque série dans l’équation, une série dont tous les termes, donc tous les coefficients doivent être nuls, ce qui va nous donner une relation de récurrence sur la suite a_i qui quelquefois, permet de trouver le terme général de S et donc d’identifier S . (Après discussion sur le rayon de convergence) .

Connaissant une solution, on utilise la méthode précédente pour en trouver une seconde .

Exemple 1 :

4xy’’ + 2y’ – y = 0

On suppose y = a₀ + a₁ x + …+a _n xⁿ + …. On dérive 2 fois, on reporte dans l’équation .

On suppose nuls tous les termes, notamment le terme en xⁿ (égalité à 0 indépendante de x).

La récurrence (2n+2)(2n+1)a_n+1 = a_n conditionne cette nullité_. On en déduit que a_n =

Si x > 0 on pose x = t² et la série de terme général t²ⁿ / (2n)! est ch t → S = a0 ch

Si x < 0 on pose x = - t² et la série de terme général (-1)ⁿ t²ⁿ / (2n)! est cos t → S = a0 cos

Dans chaque cas, on peut rechercher la seconde solution par la méthode précédente

Par exemple si on pose y = z ch on trouve z = 2k th + k₂ et finalement

y =k₁ sh + k₂ ch qui visiblement est la solution générale quand x est positif .

Type 2.7: Equations linéaires avec second membre quelconque

Revenons à

a(x)y’’ + b(x)y’ + c(x)y = f(x) (1) avec second membre

a(x)y’’ + b(x)y’ + c(x)y = 0 (2) sans second membre

Supposons qu’on connaisse 2 solutions indépendantes S₁ et S₂ de l’équation sans second membre.

Alors, la méthode de variation des constantes fonctionne et y = uS₁ + vS₂ (où u et v sont des fonctions inconnues de x vérifiant certaines conditions) est une solution de (1).

Quelles sont les conditions que doivent vérifier u et v ?

On doit avoir

y’ = u’s₁+v’s₂ + us’₁+vs’₂

Pour pouvoir résoudre notre problème, il nous faut imposer une condition supplémentaire :

u’s₁+v’s₂ = 0 (3)

Alors y’’ = u’s’₁+v’s’₂ + u’’s₁+v’’s₂ et en reportant ces résultats dans (1) :

a(x)( u’s’₁+v’s’₂) = f(x)

On obtient le système suivant :

u’s’₁+v’s’₂ = f(x)/a(x)

u’s₁+v’s₂ = 0

il s’agit d’un système classique, permettant de trouver directement les valeurs de u’ et v’

On les intègre pour trouver u et v (avec la constante d’intégration)

Et on dit que toutes les solutions sont de la forme y = uS₁ + vS_2.

On peut appliquer cette méthode dans le cas où l’équation (1) est à coefficients constants, mais dans le cas où le second membre est de la forme e^mxQ(x) avec Q polynôme, la méthode étudiée plus haut est en général plus simple.

Exemple 1 :

y’’– y = 1/ch³ x

y’’– y = 0 admet sh x et ch x comme solutions linéairement indépendantes.

On cherche une solution de type y = u ch x + v sh x

Le système à résoudre est donc :

u’ ch x + v’ sh x = 0

u’ sh x + v’ ch x = 1/ch³ x

u’ = , v’ = → u = , v = th x + k₂

y = + th x sh x + k₁ ch x + k₂ sh x