ESPACES VECTORIELS sur R

Définition

E muni d’une addition (+) et d’une multiplication par un nombre réel est un espace vectoriel sur R si pour tous les réels k, k₁ et k₂, pour tous les éléments v, v₁ et v₂ de E

● (E, +) est un groupe commutatif d’élément neutre noté 0_E (ou 0) (l’opposé de v est noté –v)

● k₁ (k₂v) = (k₁k₂) v

● (k₁+k₂)v = k₁v + k₂v

● k(v₁ + v₂)=kv₁ + kv₂

● 1v = v

L’addition des vecteurs et la multiplication d’un vecteur par un scalaire (définies avec l’espace vectoriel) ne seront pas confondues avec l’addition et la multiplication dans R bien qu’on utilise souvent la même notation.

On définit de la même façon un espace vectoriel sur C ou sur n’importe quel corps K.

Base d’un espace vectoriel

● k₁v₁ + …+ k_nv_n est une combinaison linéaire de vecteurs de E

● Dans E, n vecteurs (v₁, …v_n) sont dits linéairement indépendants si on ne peut pas trouver n scalaires k₁ , k₂ , …, k_n tels que

k₁v₁ + …+ k_nv_n = 0_E.

● Si les n vecteurs ne sont pas linéairement indépendants, ils sont liés, ce qui veut dire qu’on peut exprimer un vecteur en fonction des n – 1 autres par exemple v₁ = – 1/k₁ (k₂v₂+….+k_nv_n)

● n vecteurs linéairement indépendants forment la base d’un espace vectoriel

L’ensemble des combinaisons linéaires des vecteurs de la base a une structure d’espace vectoriel.

On dit que cet espace vectoriel est engendré par la base à partir de laquelle on l’a formé.

●Soit b = { b₁, …., b_n} un ensemble de n vecteurs linéairement indépendants de E

Si l’ensemble des combinaisons linéaires des vecteurs de b est E , on dit que b est une base de E.

Si cet ensemble est inclus dans E il forme un sous espace vectoriel de E.

● Si b = { b₁, …., b_n} est une base de E . E est dit de dimension n

● une droite vectorielle est un espace vectoriel de dimension 1 , un plan vectoriel est de dimension 2 .

Notre étude se bornera à l’étude des espaces vectoriels de dimension finie.

● Dans tout espace vectoriel, il y a forcément le vecteur nul (combinaison linéaire avec n scalaires nuls).

Dans un espace vectoriel de dimension n , tout ensemble de n + 1 vecteurs est lié

Dans cet espace vectoriel, toute ensemble de n vecteurs linéairement indépendants est une base.

● Tout vecteur est écrit comme une combinaison linéaire unique des vecteurs de sa base et les scalaires de cette combinaison linéaire sont appelés coordonnées

● Dans E v = x₁b₁ + x₂b₂ + ….+ x_nb_n (x_i coordonnées de v dans la base b)

● Le vecteur b _i peut être considéré comme un vecteur dont toutes les coordonnées sont nulles sauf la i^ème qui est égale à 1.

b _i = (0, 0, …., 0 , 1, 0, …., 0)

Changements de base

● Dans un espace vectoriel, E, on peut choisir une infinité de bases.

● Dans la base b un vecteur de E s’écrit de façon unique v = x₁b₁ + x₂b₂ + ….+ x_nb_n

● Si on change de base, un vecteur change de coordonnées .

● pour changer de base, il faut qu’on nous donne la nouvelle base b’ en fonction de l’ancienne b

On a par exemple

b’₁ = a₁₁b₁+……a_1nbn

( ……………………. ) (n équations)

b’_n = a_n1b₁ + …+ a_nn b_n

● On résout le système pour trouver b₁, …., b_n dans la base b’

b₁ = A₁₁b’₁+……A_1nb’n

( ……………………. ) (n équations)

b_n = A_n1b’₁ + …+ A_nn b’_n

● Puis, dans v = x₁b₁ + x₂b₂ + ….+ x_nb_n on remplace b₁, …., b_n par leur valeur dans la base b’

● Et on trouve v = x’₁b’₁ + x’₂b’₂ + ….+ x’_nb’_n

où x’₁, …,x’_n sont les nouvelles coordonnées de v dans la base b’

● L’application qui dans R ⁿ fait correspondre aux coordonnées d’un vecteur (x₁ , x₂ , …., x_n) dans la base b les coordonnées du même vecteur dans la base b’ (x’₁, x’₂, …., x’_n) est une application bijective.

Ce qui signifie qu’il existe un changement de base réciproque nous faisant passer de la base b’ à la base b.

F sous espace vectoriel de E

Une partie F de E est un sous espace vectoriel si elle a une structure d’espace vectoriel.

● Pour démontrer que F est un SEV il suffit de démontrer que F est stable pour les lois de E c'est-à-dire :

Tout V ∈ F et tout k ∈ R ➜ kV ∈ F

Tout V₁ ∈ F et tout V₂ ∈ F ➜ V₁ + V₂ ∈ F

Les autres propriétés sont implicites puisque héritées de E.

● Tout SEV contient forcément le vecteur nul

● Le vecteur nul forme à lui tout seul un SEV.

● Dim (F) ≤ Dim (E) (E peut être considéré comme un SEV de lui-même)

● Si Dim (F) = p et Dim (E) = q , si b = { b₁, …., b_p} est une base de F alors on peut former une base de E en adjoignant à la base b de F

q – p vecteurs {b _{p+1 ,} …., b _q} tels que le système b’ ainsi formé soit libre.

● De la même façon, il existe une base b’ de E b’ = { b₁, …., b_q} telle qu’on puisse en extraire p vecteurs qui forment une base de F.

● Les plans vectoriels et les droites vectorielles sont des SEV d’un espace vectoriel de dimension 3.

● Seules les droites vectorielles parallèles à un plan sont des SEV de ce plan (une droite vectorielle qui n’est pas parallèle au plan n’est pas contenue dans le plan).

Applications dans les espaces vectoriels

Dans le cas général E est un espace vectoriel rapporté à une base b

F est un espace vectoriel rapporté à une base b’

E et F ne sont pas forcément de même dimension. Par exemple Dim (E ) = n et Dim (F ) = q .

Une application f de E dans F fait correspondre à un vecteur V de E un vecteur image V’ dans F

f : E ➜ F

f : V ➜ V’ = f(V)

● On peut définir f de multiples façons mais la plus courante et celle qui permet de déterminer les coordonnées de V’ dans la base b’ en fonction des coordonnées de V dans la base b.

(x₁ , x₂ , …., x_n) ➜(x’₁, x’₂, …., x’_p)

On aura donc p équations pour définir (x’₁, x’₂, …., x’_p) en fonction de (x₁ , x₂ , …., x_n).

● On peut aussi définir des applications dans E (F = E) ou de E dans une partie de E, rapportés à une même base ou à des bases différentes.

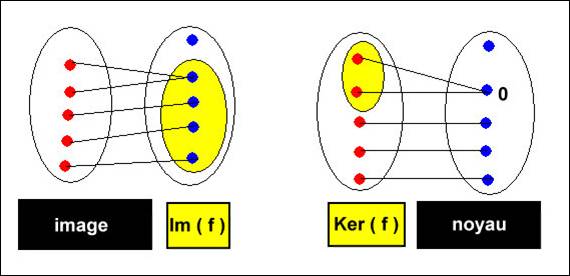
● On appelle image de f notée Im ( f) l’ensemble des images des éléments de E données par f .

On peut écrire Im ( f) = f ( E) . C’est soit F soit un sous ensemble de F .

Si f est surjective Im ( f ) = F

● On appelle noyau de f , noté Ker ( f ) , l’ensemble des éléments de E qui ont pour image 0_F .

Si f est injective Ker ( f ) est réduit à un seul élément qui n’est pas forcément 0_E .

Exemples d’espaces vectoriels

● Les vecteurs du plan (base { i , j } , coordonnées X et Y telles que V = X i + Y j )

● Les polynômes de degré ≤ 2 à coefficients dans R (base x² , x , 1}, coordonnées les coefficients a, b , c )

● R² (base {( 1 , 0) , (0, 1) } coordonnées a, b tels que a.(1, 0) + b .(0,1) = (a , 0) + (0 , b) = (a , b) )