Déterminant d’une matrice carrée

Ordre 2 :

le déterminant de M = est noté et évalué à det (M) = ad – bc

Le déterminant d’une matrice est donc un nombre réel obtenu en combinant ses coefficients selon une recette particulière.

Ceci dit, on va voir que quand on sait calculer le déterminant d’ordre n , on sait aussi calculer le déterminant d’ordre n+1.

Ce qui signifie que si l’on sait calculer un déterminant d’ordre 2, on va pouvoir, sans trop de difficultés, calculer les déterminants d’ordre 3, 4, et plus.

Ordre 3 :

Comment calculer le déterminant suivant  ?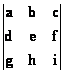

● Les signes affectés aux coefficients (signes de position) seront :

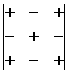On attribue un + à a₁₁ puis on alterne dans une ligne ou colonne quand l’indice croit

● En barrant la 1ere colonne et successivement la 1ere ligne puis la 2^e , puis la 3^e , comme dans l’encadré ci-dessous, ce qui reste visible dans chaque cas est une matrice d’ordre 2 dont on sait calculer le déterminant .

On calcule ce déterminant affecté du signe de position de a _{i k} et on appelle le résultat

cofacteur de a _{i k ,} a _{i k} étant le coefficient de la première colonne dont la ligne a été barrée.

Le cofacteur de a _{i k} est un nombre que nous noterons c ( i , k )

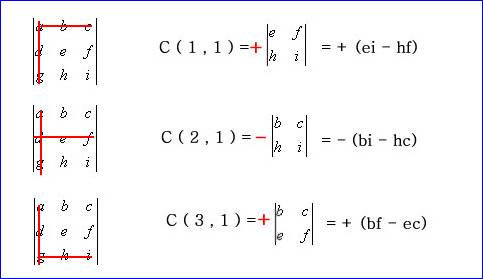
● Le déterminant de la matrice d’ordre 3 est égal à la somme des a _{i k} . c(i,k)

det (M) =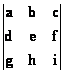 = = +a (ei – fh) – d ( bi – hc)+ g (bf – ec)

● cette façon de faire utilise pour le calcul exclusivement les coefficients de la 1ere colonne et leur cofacteur.

On dit qu’on développe le déterminant par rapport à la première colonne mais on aurait pu le développer de la même façon par rapport à n’importe quelle colonne ou n’importe quelle ligne.

● Si on développe le déterminant par rapport à la 1ere colonne, il revient au même d’affecter à a le signe + , à d le signe – et à g le signe + . On multiplie chaque coefficient affecté de son signe par le déterminant de la matrice d’ordre 2 qu’on obtient en barrant la ligne et la colonne du coefficient et on fait la somme.

Mais on ne perd pas de vue qu’en réalité c’est c ( i , k) qui intègre le signe de position.

Chaque coefficient de la matrice a un cofacteur construit en affectant de son signe de position le déterminant obtenu quand on barre sa ligne et sa colonne.

Par exemple, c (2 , 2) cofacteur de a₂₂ est

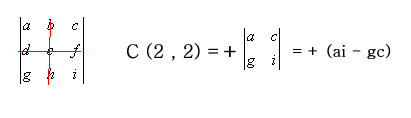
● Tout coefficient ayant un cofacteur ; il est possible de développer le déterminant par rapport à n’importe quelle ligne ou colonne, mais exclusivement par rapport à une ligne ou à une colonne.

Dans chaque cas, le déterminant calculé sera le même nombre.

Plus il y a de 0 dans une ligne ou une colonne plus on a intérêt à développer le déterminant par rapport à elle. Les calculs s’en trouvent facilités.

Remarques :

● Quel que soit l’ordre de la matrice, la règle qui permet d’affecter les signes de position est la même

● On peut définir un déterminant d’ordre 1 comme le nombre qui reste visible quand on barre une ligne et un colonne dans une matrice d’ordre 2 . Dans ce cas, la procédure qui nous permet de calculer un déterminant d’ordre 2 connaissant les déterminants d’ordre 1 est la même que celle qui nous permet de calculer un déterminant d’ordre 3 connaissant les déterminants d’ordre 2.

Quand on sait calculer un déterminant d’ordre 3 , on sait calculer un déterminant d’ordre 4 .

● Par récurrence, on peut calculer tous les déterminants quel que soit leur ordre.

Propriétés des déterminants

● Si on appelle L1, L2 , L3 les vecteurs lignes de la matrice M et C1, C2, C3 ses vecteurs colonnes qu’on sait appartenir à l’espace vectoriel Rⁿ (Kⁿ dans le cas général) .

On peut noter det (M) soit det (L1, L2, L3) soit det (C1, C2, C3)

Alors, on a det (L1, L2, L3) + det (L1, L’2 , L3) = det (L1, L2+L’2 , L3)

Idem pour les colonnes

Et det (L1 , λL2 , L3) = λ det (L1, L2 , L3)

Idem pour les colonnes.

Donc si A et B sont des vecteurs fixes et X un vecteur variable

on peut considérer que l’application X → det (A, X, B) est une application linéaire de Rⁿ dans R .

● Règle importante : si le déterminant d’une matrice est non nul, la matrice est inversible et si il est nul, la matrice n’est pas inversible

Pratiquement

● Si deux lignes sont identiques ou si l’une est le produit de l’autre par un scalaire

(L3 = λL1 ) ( système lié , matrice non inversible), le déterminant est nul

det (L1, L1, L3) = 0

● Donc , si on ajoute à une ligne une combinaison linéaire des autres le déterminant est inchangé

det (L1, L2+K₁L1+K₂L3 , L3) = det (L1,L2,L3) + K₁ det (L1,L1,L3) + K₂(L1,L3,L3) = Det(L1,L2,L3)+0+0

● On a donc intérêt à ajouter à une ligne (ou colonne) d’autres lignes ou combinaisons d’autres lignes (ou colonnes) pour obtenir un maximum de coefficients nuls dans cette colonne et développer le déterminant par rapport à cette ligne (ou colonne). Le calcul en sera facilité.

● Si on échange deux lignes le déterminant est multiplié par –1 :

det(L1,L2,L3) = – det (L2,L1,L3)

En effet :

det(L1,L2,L3) = det(L1+L2,L2,L3)=det(L1+L2, -L1,L3)=det(L2,-L1,L3) = – det(L2,L1,L3)

On remplace L1 par L1+L2 puis L2 par L2 – (L1+L2) , puis L1+L2 par (L1+L2) – L1, puis linéarité

● Si A est une matrice de M _n det(λA) = λⁿ det (A)

● le déterminant d’une matrice triangulaire est égal au produit des coefficients de sa diagonale

Calcul de la matrice inverse à partir des cofacteurs et du déterminant

Cofacteurs

Quand je développe le déterminant par rapport à la colonne 1 j’ai une formule du type

Det (M) = a _{11 .} C( 1, 1) + a ₁₂ . C (1,2) + …. + a _{1n .} C(1,n)

C( i , k ) incluant le signe de position

Idem quand je développe le déterminant par rapport à une autre colonne ou à une autre ligne.

Donc, à chaque a _ik il correspond un nombre C ( i , k ) qu’on appelle son cofacteur .

C’est le déterminant obtenu en supprimant la ligne i et la colonne k , affecté du signe de position .

Cofacteurs et matrice inverse

En calculant tous les cofacteurs, je peux faire correspondre à la matrice M une matrice dont les coefficients b _ik sont de la forme . J’appelle cette matrice m .

● On obtient la matrice transposée ^tM d’une matrice M en échangeant ses coefficients

a _ik et a _ki ce qui revient à construire la matrice symétrique de M par rapport à la diagonale principale.

● la transposée de m (dérivée de M grâce aux cofacteurs divisés par le déterminant de M) est M^-1 matrice inverse de M.

● Exemple

M = admet pour cofacteurs et pour déterminant det(M) = 2 – 3 = – 1

La matrice correspondante m obtenue grâce aux cofacteurs divisés par le déterminant est

m = .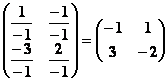

La transposée de m est . C’est M^–1

En effet si

X = 2x + 3y on a aussi x = –X + 3Y

Y = x + y y = X – 2Y

(Matrice M) (Matrice M^–1)

Ceci dit, on a plus vite fait de résoudre le système en considérant que X et Y sont connus et x et y inconnus.