Approximations et développements limités

Fonction négligeable devant une autre ou équivalente à une autre

● h(x) négligeable devant f(x) quand x →a si  = 0 .  Noté h   f  (a peut être ± ∞ )

Le signe n’intervient pas, seul l’ordre de grandeur,  et +∞ peut être négligeable devant –∞.

Relation transitive : h << g et g << f    ⇒     h << f

● h(x) équivalente à f(x) quand x →a si   = 1 . Noté h   f  (a peut être ± ∞ )

ou  bien encore :  h   f   si     f(x) = h(x) (1 + ε (x))     et    ε (x) = 0

●   Relation d’équivalence : Réflexive, symétrique,  transitive

● Compatible avec <<    car     h << f et  f » F      ⇒        h << F

Seuls équivalents admis :

● Si   f » F et g » G          alors           fg » FG          et          f/g   » F/G  

● Si f << g    alors   f + g   »   g  

● d’où on tire   si f << g et F << G       alors         

● si f » F    alors   f ^a »  F ^a  (tout ⍺ ∈ R)

Les autres équivalents sont à démontrer et à manier avec précaution

Notation de Landau

o (f) : se lit fonction négligeable devant f

Si j’écris pour x prés de 0 : sin x = x + o(x²) cela signifie sin x  – x << x²

Mais attention : plusieurs fonctions différentes négligeables devant f s’écrivent toutes o(f) .

On peut donc avoir par exemple o(f) + o(f) = o(f)

Aussi pour les calculs, on peut remplacer o(f) par ε(x).f(x) (avec lim ε = 0) et changer de ε à chaque approximation.

Développements limités

Echelle : Base de référence pour le classement de fonctions usuelles dans la relation <<

Echelle des fonctions négligeables l’une par rapport à l’autre à l’infini  (à connaître)  

   <<   1   <<   ln x    <<    x   <<    x²     << …….<<   xⁿ (n > 2)    <<     e^x     <<   a^x  (a > e)

Echelle des fonctions négligeables l’une par rapport à l’autre prés de 0  (à connaître)

xⁿ    <<   …..   <<    x²      <<  x      <<   1    <<    ln x    <<    

On peut construire des échelles plus riches et intercaler par exemple les fonctions x^⍺ (ln x)^β

Partie principale de f

Soit C une constante

Définition : On dit que Cf₀ est la partie principale de f si f₀ fait partie de l’échelle et f » Cf₀ .

                    On peut écrire que f = Cf₀ + o(f₀) .

                     On peut provisoirement la noter PP(f) = Cf₀  (notation personnelle)

Par exemple pour un polynôme de degré n , à l’infini,  a_nxⁿ est sa partie principale C = a_n .

À l’infini, sin x n’a pas de partie principale mais sin x admet x pour partie principale en 0 .

● le C de Cf₀ est unique

● PP(f.g) = PP(f) . PP(g) 

● PP(f/g) = PP(f) / PP(g)

● Si PP(f) + PP(g) ≠ 0 alors

               PP(f+g) = Sup (PP(f) , PP(g)) dans l’échelle ou PP(f)+PP(g) si elles sont du même ordre

 Développement asymptotique de f

Dans ce qui suit les fonctions f _i sont dans une échelle avec f_n << f_n–1 << ……<< f₀

1 On a C₀f₀ = PP (f)

2 Puis on trouve C₁f₁ = PP (f - C₀f₀ )    approximation de l’erreur

3 Puis on trouve C₂f₂ = PP (f - C₀f₀ - C₁f₁)

4 et ainsi de suite jusqu’à C_nf_n = PP (f – C₀f₀ – C₁f₁ – …..– C_n–1f_n–1 )

5 On en déduit que f =  C₀f₀  + C₁f₁ +…..+ C_n–1f_n–1 + C_nf_n + o(f_n)

Développement asymptotique de f d’ordre n dans l’échelle choisie

● si l’échelle est celle des xⁿ et que nous nous situions au voisinage du 0 nous avons un développement limité de f à l’ordre n en 0 . Que nous abrègerons en DL_n(f).

f(x) = a₀ + a₁x + …..+a_nxⁿ + o(xⁿ) = P(x) + o(xⁿ) où P(x) est un polynôme de degré n .

Ce polynôme est unique du fait de l’unicité des a_i définissant chaque PP.

On dit soit que P(x) est un DL_n (f) soit que f(x) = P(x) + o(xⁿ) si on veut être plus précis.

● toutes les fonctions n’ont pas un DL_n en 0 et il arrive, selon l’ordre du développement qu’il faille prendre x très petit pour que  o(xⁿ) devienne vraiment négligeable devant xⁿ , le voisinage de 0 étant une notion arbitraire.

Développements limités fondamentaux (en 0 )

À connaître par cœur car souvent utiles

Opérations sur les fonctions et DL

Les DLn sont en général compatibles avec les opérations courantes sur les fractions

● DL (f+g) = DL (f ) + DL (g)

● DL (f.g) = DL(f ) . DL (g) à condition de supprimer les termes de degré > n

● DL (f/g) = DL (f) / DL (g)  (si on sait diviser le polynômes et que le dénominateur n’est pas nul)

● On peut faire un changement de variable de type X = Kx^⍺ (si x → 0 c’est aussi le cas de X)

● DL ( g ○ f) = DL (g (f(x)) n’est possible que si f(0) = 0 . Dans DL(g) on remplace x par DL(f) .

 Formules de Taylor

Si

f continûment dérivable jusqu’à l’ordre n sur [a ; b] (donc de classe Cⁿ) et f⁽ⁿ⁾ est dérivable sur [a ;b]

Si h est tel que a < a+h ≤ b ,  Il existe θ  (0 < θ < 1 donc a< (a+ θh) < (a + h) tel que

f(a+h) = f(a)  +  hf⁽¹⁾(a) + 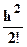 f⁽²⁾(a)+…+ 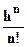f⁽ⁿ⁾(a)  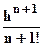 +   f⁽ⁿ⁺¹⁾(a+θh)    Taylor Lagrange

En particulier si on remplace h par (b – a) on trouve f(b) = …

f(h) = f(0)  +  hf⁽¹⁾(0) + 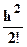 f⁽²⁾(0)+…+ 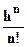f⁽ⁿ⁾(0)  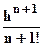    +  f⁽ⁿ⁺¹⁾(θh)     Mac Laurin 

C’est la même formule avec a = 0 et dans ce cas on peut remplace h par x pour trouver

f(x) = f(0)  +  xf⁽¹⁾(0) +  f⁽²⁾(0)+…+ f⁽ⁿ⁾(0)      +  f⁽ⁿ⁺¹⁾(θx)

● Si on se situe maintenant au voisinage de 0 et que f⁽ⁿ⁺¹⁾ soit bornée , le dernier terme de la somme devient tel que

f⁽ⁿ⁺¹⁾(θx) << xⁿ et on peut écrire le DLn :

f(x) = f(0)  +  xf⁽¹⁾(0) +  f⁽²⁾(0)+…+ f⁽ⁿ⁾(0)      + 0(xⁿ)

 C’est de là que proviennent les DLn.

Quelques utilisations de DL

Pour se livrer aux opérations suivantes, il faut absolument que f soit de la classe Cⁿ

● Si f est bijective, on sait que f^–1 est de classe Cⁿ

On pose DL (f^–1 ) = a_nxⁿ +….+a₀ .(a _i inconnus)

Puis on écrit que DL(f ○ f^–1) = x en remplaçant dans le DL(f) x par a_nxⁿ +….+a₀ .

Ensuite, on identifie dans DL(f ○ f^–1)  les coefficients à 0 sauf celui de x qui est égal à 1.

On trouve ainsi un DL de f^–1 .

● On peut dériver le DL de f pour trouver celui de f’ (par exemple sinx et cos x)

● On peut prendre la primitive du DL de f pour trouver le DL de cette primitive F

Suites et développements de fonctions de C^¥ dont le reste tend vers 0

On retrouve dans la suite U_n =1 + 1 + 1/2 ! + 1/3! + …+1/n! le développement limité de e^x pour x=1 mais 1 n’est pas au voisinage de 0 . On se tourne alors vers Mac Laurin et on estime le reste :

e^θ / n !  avec 0 < e^θ < 1. Ce qui nous permet de dire que le reste → 0 et que la suite converge vers e.

Calcul de limites en zéro :

On a souvent intérêt à substituer les DL aux  fonctions usuelles. (quand ils ont connus).

DL au voisinage d’un point

● Si on prend une échelle prés de 0

xⁿ    <<   …..   <<    x²      <<  x    

On peut la transformer en échelle « prés de a » en remplaçant x par (x-a)

(x-a)ⁿ    <<   …..   <<    (x-a)²      <<  (x-a)

Taylor (ou Mac Laurin) donnent alors dans le voisinage  de a

f(x) = f(a)  +  (x-a)f⁽¹⁾(a) +  f⁽²⁾(a)+…+ f⁽ⁿ⁾(a)   +   f⁽ⁿ⁺¹⁾(a+θ(x-a))

Et si f ⁽ⁿ⁺¹⁾ est bornée, on a un développement limité au voisinage de a .

Position du graphe de f par rapport à sa tangente en a

L’équation de la tangente à f en a est T(x) = T(a) + (x-a) f⁽¹⁾(a) et comme T(a) = f(a), on reconnaît les premiers termes de la formule de Taylor T(x) = f(a) + (x-a) f⁽¹⁾(a).

On en déduit que  f(x) –T(x) = f⁽²⁾(a)+…+ f⁽ⁿ⁾(a)+… et au voisinage de a l’étude du signe

de f(x) –T(x) se résout à l’étude du signe du  1^er terme non nul de cette suite.

● Si f⁽²⁾ (a) n’est pas nul, (x-a)² étant positif  f(x)-T(x) est du signe de f⁽²⁾ (a) que x soit plus grand ou plus petit que a. Donc, localement, la courbe est soit toute au dessus (f(x)-T(x)>0) , soit toute au dessous (f(x)-T(x) <0)  de la tangente.

● Si f⁽²⁾ (a) est nul, le signe de f(x) – T(x) est donné par le signe du 1^er  f⁽ⁿ⁾(a) non nul.

Si ce terme est de degré impair, la courbe traverse la tangente puisque le signe de f(x) – T(x) change à droite et à gauche de a (on a un point d’inflexion) . Si il est de degré pair, la courbe reste du même côté de la tangente.

D’un DL à un autre

● Au voisinage de 0

on sait que  = 1 –x +x²–x³+..+(–1)ⁿxⁿ

On peut  écrire f(x)=  et diviser le DL de  par .

Pour trouver  que f(x) = x ^–1/2 –x^1/2 +x^3/2 + o(x^3/2)

Les puissances fractionnaires de x qui figurent dans cette somme constituant un échelle décroissante au voisinage du 0 .

● Quand x tend vers l’infini

Quel est le comportement à l’infini de f(x)=  ?

Si dans  quand x → 0 je fais le changement de variable x =  quand X →∞  

J’obtiens = 1 –  + – +… d’où  =  – + –+…

Donc f(x)=  = (X  -1 +–+..) +  ( – + –…) = X  -1 + – +…

Et on retrouve l’asymptote oblique de f , la droite d’équation y = X – 1 , le reste étant négligeable.

Mais plutôt que de procéder ainsi, on peut simplement faire la division de X²+1 par X+1 et on trouvera le même résultat sans changement de variable.

Remarquons que dans un développement à l’infini, on range les termes par puissances décroissantes de x , le « polynôme » se comportant comme ses termes de plus haut degré.