APPLICATIONS

Définitions et propriétés:

Dans ce qui suit A ➩B se lit « A implique B »

X → Y Traduit une correspondance entre X et Y

● Une RELATION R établit un lien entre les éléments d’un ou plusieurs ensembles. Pour signifier que deux éléments x et y sont en relation par R, on écrit x R y , ce qui n’implique pas obligatoirement y R x .

Exemples de relation dans Z : R : «  x est plus grand ou égal à y ». Au lieu d’écrire x R y on écrit x ≥ y.

: « x est égal à y » qu’on écrit x = y

: « x est égal à y modulo 7 si en faisant la division euclidienne x et de y par 7 on trouve le même reste » qu’on écrit x = y mod 7

● Une relation peut être

symétrique Pour tout couple (x,y) d’éléments en relation : x R y ➩ y R x (exemple A = Y ➩Y = A)

antisymétrique : Pour tout couple (x,y) d’éléments en relation : x R y et y R x ➩ x = y (exemple X ≤ Y et Y ≤ X ➩ X = Y )

réflexive : Pour tout élément x on a x R x (exemples X ≤ X ou X = X)

transitive : Pour tout triplet (x, y , z) d’éléments en relation : x R y et y R z ➩ x R z (exemple X ≤ Y et Y ≤ Z ➩ X ≤ Z)

● Une relation d’ordre est antisymétrique , réflexive, transitive (exemple £ est une relation d’ordre)

● Une relation d’équivalence est symétrique, réflexive, transitive (exemple a = b modulo q si la division de a et de b par q donne le même reste r)

(On appelle classes d’équivalence les sous ensembles d’éléments qui sont en relation entre eux)

(exemple tous les nombres dont le reste de la division par q est r forment une classe d’équivalence, sont équivalents entre eux)

● Une APPLICATION f de E dans F est une relation qui met en correspondance tout élément de E avec un élément de F et un seul . f est une application de E dans F s’écrit : f : E → f

Quand x et y sont en relation par une application, on écrit y = f(x). y est l’image de x et x l’antécédent de y.

● Rappel E X F ensemble produit de E par F est l’ensemble des couples (x,y) tels que x ∈ E et y ∈ F.

E X E est noté E ^{2 .}

Le sous ensemble de E X F formé des couples (x, f(x)) est appelé graphe de f .

● Quand l’ensemble d’arrivée est un ensemble de nombres R ou C ,

on dit que l’application est une fonction numérique.

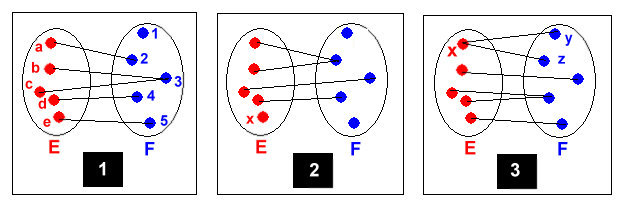
1 Application 2 Non application 3 Non application

Tout élément à une image x n’a pas d’image x a 2 images y et z

et une seule.

● une application de E dans F est dite injective si tout (x,y) ∈ E X E : x ≠ y ➩ f(x) ≠ f(y)

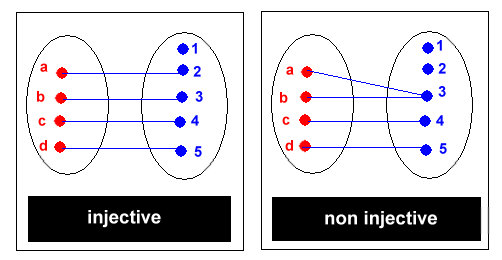
2 éléments distincts de l’ensemble de départ doivent avoir 2 images distinctes dans l’ensemble d’arrivée.

● Une application est dite surjective si tout élément de F a au moins un antécédent dans E

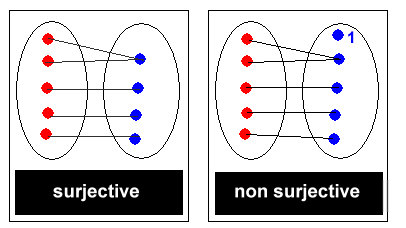
Tout élément de l’ensemble d’arrivée doit être l’image d’au moins un élément de l’ensemble de départ.

● une application à la fois surjective et injective est dire bijective

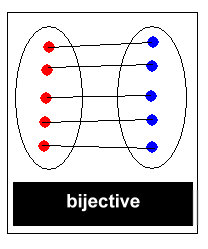
Tout élément de l’ensemble de départ a une image et une seule dans l’ensemble d’arrivée.

ET

Tout élément de l’ensemble d’arrivée est l’image d’un élément et d’un seul de l’ensemble de départ.

Une application n’est pas bijective si elle est non injective ou non surjective.

Soit f une application numérique de E dans F

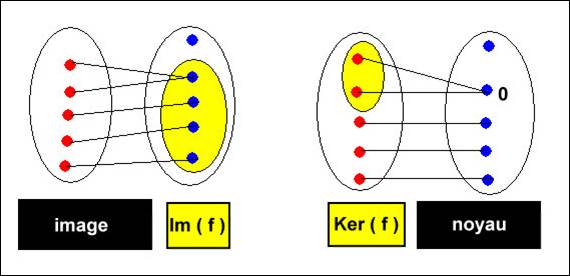
● on appelle image de f (noté Im ( f ) ) l’ensemble des éléments de F ayant un antécédent par f .

● on appelle noyau de f (noté Ker ( f ) ) l’ensemble des éléments de E ayant pour image le 0 de F .

Si f est bijective

● Quand E (ou F) est un ensemble fini E et F possèdent le même nombre d’éléments. Card (E) = card (F)

● Il existe une application réciproque de f notée f ^-1 .

f ^-1 est une application de F dans E définie par : tout y ∈F : si y = f(x) alors x = f ^-1 (y).

f ^-1 ○ f = f ○ f ^-1 = I (identité)

● l’image de E par f : f (E) = F et f ^-1 (F) = E . Im (f ) = F.

● Le noyau { ensemble des x tels que f^- (x) = 0 } que l’on peut aussi noter f ^-1 ({0}) se réduit à un seul élément

Composée de deux applications :

Composer deux applications c’est les appliquer l’une après l’autre dans un ordre déterminé.

Soit f une application de E dans F et g une application de F dans G .

Pour composer f et g dans cet ordre , il faut que l’ensemble de départ de g soit l’ensemble d’arrivée de f .

Dés lors on définit l’application g ○ f de E dans G de la façon suivante

g ○ f : E → G

g ○ f : x → z = g ○ f (x) | g ○ f (x) = g ( f (x ) ) . f(x) est l’antécédent de z par g .

Ce qu’on peut représenter par le schéma suivant :

E → F → G

x f f(x) g g○f (x)

Attention ! quand on écrit g○f la première application en action est celle qui est écrite à droite : f

En général g○f est différent de f○g

Pratiquement on appelle application composée une application usuelle où on a remplacé X par une application de X .

on appelle fonction composée une fonction usuelle où on a remplacé X par une fonction de X .

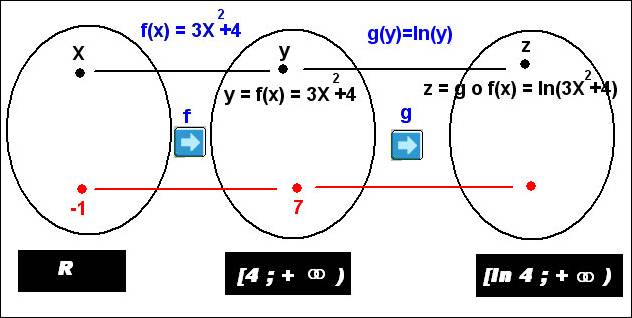
Par exemple g(x) = ln (x) est une fonction usuelle. (logarithme népérien de X)

h (x) = ln(3x² +4) est une fonction composée puisque dans g(x) j’ai remplacé X par 3x² +4.

Si je pose f(x) = 3x² +4 je peux écrire h(x) = g(3x² +4) ou encore h(x) = g(f(x)) ou encore h(x)= g○f (x) ou encore h = g○f

Dérivées :

● Dérivée d’une fonction composée

On connaît la fonction usuelle sin (x )

On peut considérer la fonction sin (x² + 2) comme la composée de :

f : x →x² + 2 et g : x → sin (x)

g○f (x) = g(f(x) = sin(f(x)) = sin (x² + 2)

La règle de dérivation de g○f (x) par rapport à x est la suivante

La dérivée de g○f (x) par rapport à x est égale au produit de la dérivée de g par rapport à f par la dérivée de f par rapport à x .

1) si on considère f comme une variable, on sait dériver g (f ) par rapport à f :

g( f) = sin (f) , donc sa dérivée par rapport à f est g’ (f ) = sin’ (f) = cos (f)

2) f étant une fonction simple de x, on sait dériver f par rapport à x :

f ( x ) = x² + 2 , donc sa dérivée par rapport à x est f ’(x) = (x² + 2)’ = 2x

3) La dérivée de g○f (x) par rapport à x est égale au produit de ces deux dérivées

[g○f (x) ] ^‘ = [ cos (f) ] [ 2x]

et si on remplace f par sa valeur [g○f (x) ] ^‘_x = [sin (x² + 2)] ‘ = 2x cos (x² + 2)

● dérivée d’une fonction réciproque f^-1 connaissant la dérivée de f

Quelle est la dérivée de la fonction y = arcsin (x ) fonction réciproque de sin(x) ?

Si on prend x dans l’intervalle [ - π/2 ; + π/2] on a y = sin (x ) et x = arcsin (y) .

Si on dérive x = arcsin (y) par rapport à x, en utilisant la dérivation des fonctions composées on obtient :

Dérivée de x par rapport à x = dérivée de arcsin(y) par rapport à y multipliée par dérivée de y par rapport à x

Soit 1 = [arcsin(y)]’_y . y’_x .

Il revient au même de chercher la dérivée de arcsin(y) par rapport à y ou celle de arcsin(x) par rapport à x.

Donc la dérivée cherchée est [arcsin(y)]’_y = car si y = sin(x) → y’ = cos(x).

Il ne me reste plus qu’à exprimer cos(x) en fonction de y et comme sin²(x) + cos²(x) = y² + cos²(x) = 1

Cos(x) = donc la dérivée de arcsin(y) par rapport à y est , ou ce qui revient au même :

(arcsin(x))’ =

Plus généralement

Pour chercher (f^–1)’ connaissant f’

1 ) on écrit x = f^–1_(y)

2) on dérive par rapport à x 1 = [ f^–1(y) ] ‘_(y) . y’_(x)

3) on a donc [ f^–1(y) ] ‘_(y) =

4) il suffit de calculer f ’(x) en fonction de y et on a [ f^–1(y) ] ‘_(y) en fonction de y

5) ce qui revient au même que de connaître la dérivée de f^–1(x) en fonction de X (si on le souhaite on peut dire que y s’appelle x ou autrement )

Ensembles d’applications

On peut définir l’ensemble des applications de E dans F ( F (E,F) ) ou des applications dans E (F (E)) .

Dans F (E) , la composition d’application (loi ○ ) peut être considérée comme une loi de composition interne dont l’identité est l’élément neutre. .